
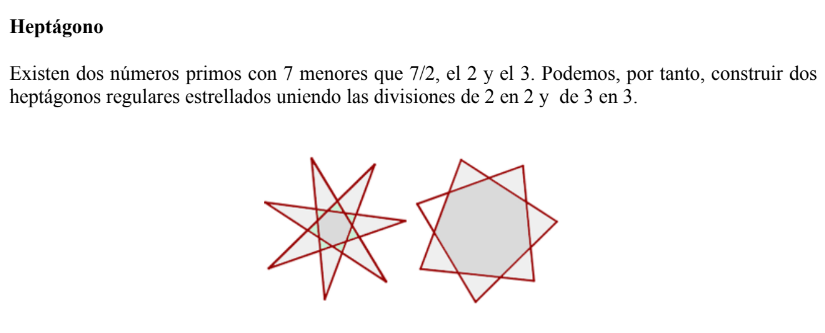
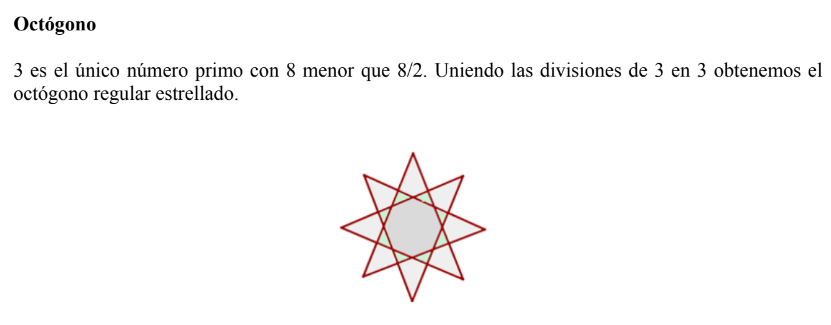
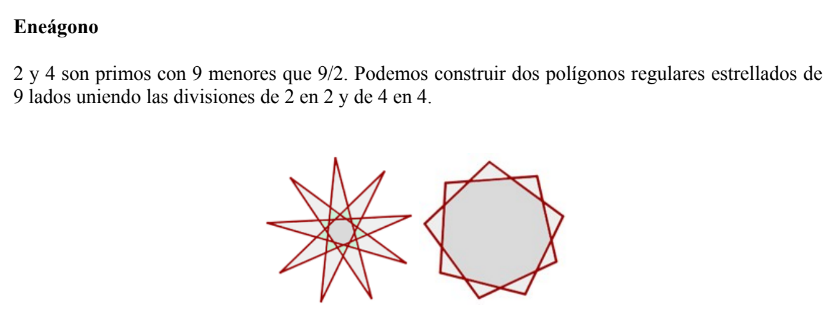
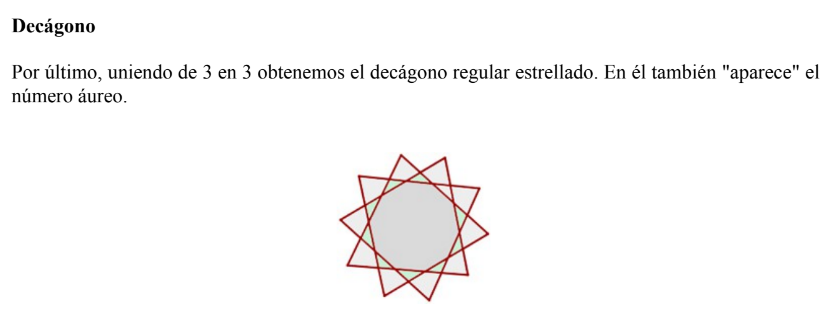
Si dividimos una circunferencia en partes iguales y unimos los puntos divisorios de dos en dos, o de tres en tres, etc, y se cierra la poligonal después de recorrer la circunferencia un número entero de veces, el resultado será un polígono regular estrellado.
Suponiendo que la circunferencia está dividida en n partes iguales y que se unen las divisiones de k en k , con k>1, se obtendrá un polígono regular estrellado de n lados si, y sólo si, n y k son primos entre sí, es decir, siempre y cuando n y k no tengan divisores comunes distintos de la unidad.
Como unir divisiones de k en k es como unirlas de n-k en n-k, se podrán construir polígonos estrellados considerando los números naturales menores que n/2 que sean primos con n.
Algunos polígonos estrellados:

Observación: no existen hexágonos estrellados de trazo único, ya que no hay ningún número primo con 6 menor que 3.
Haciendo uso de la fracción mediadora, obtendremos el grado de pureza de la mezcla de forma inmediata.

¿Cómo se mueven las bolas? ¿Se mueven en círculo o en línea recta? Describe los distintos movimientos.

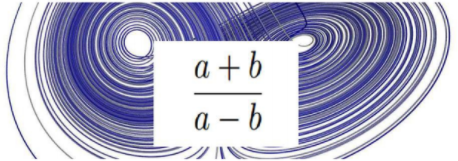
Sean a y b dos números reales tales que 2a2 + 2b2 = 5ab. Halla los posibles valores de la siguiente expresión:
El matemático y divulgador Marcus du Sautoy habla sobre la presencia de la simetría en la vida real y nos descubre al también matemático Évariste Galois cuando habla de la manera de estudiar y organizar matemáticamente las distintas simetrías de un mismo objeto.
Página 69 de 93
