Inicio

Dos estudiantes de la Universidad de Sheffield -Nicole Wrightham y Alex Craig- han encontrado la fórmula matemática que permite la decoración perfecta del árbol de Navidad. La solución que ellos proponen es la siguiente:

- Para determinar el número de adornos apropiado para tu árbol toma la raíz cuadrada de 17, divide entre 20 y multiplica por la altura del árbol en centímetros.

- Las típicas cintas de colores brillantes deben tener esta medida: 13xPI dividido entre 8, el resultado multiplícalo por la altura del árbol y ya tienes la longitud de la cinta en centímetros.

- Las luces: multiplica la altura del árbol en centímetros por PI para calcular cómo de larga tiene que ser la ristra de bombillas que vas a necesitar.

- Si vas a colocar un ángel también puedes calcular su altura: divide entre 10 la altura del árbol en centímetros.

Teóricamente, con estas medidas puedes adornar cualquier árbol, sea uno pequeño, como el de tu casa, o el árbol gigante que instala el ayuntamiento de tu ciudad. Si quieres probarlo, ¡adelante!

Y si no, siempre te quedará la opción de diseñar un árbol de Navidad al estilo matemático como el que forman las siguientes igualdades de números enteros:

Un fractal es un objeto cuya estructura se repite a diferentes escalas. Es decir, por mucho que nos acerquemos o alejemos del objeto, observaremos siempre la misma estructura.

El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal, como ocurre por ejemplo en el romanesco.

::::::

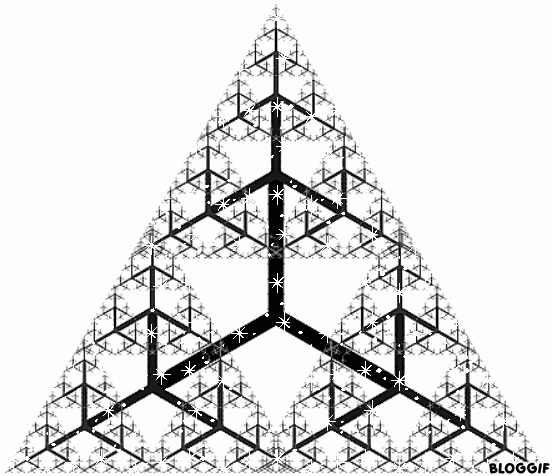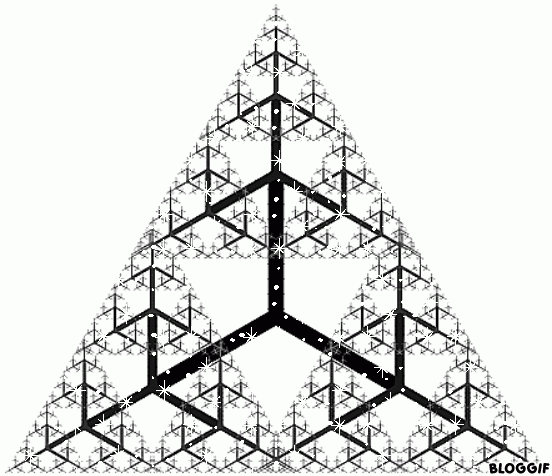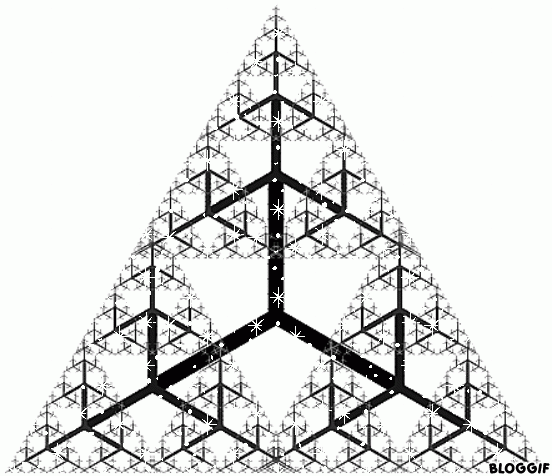
El principio del palomar, también llamado principio de Dirichlet, establece que si n palomas se distribuyen en m palomares y n > m, entonces habrá al menos un palomar con más de una paloma. Resulta evidente que si tenemos que colocar unas cuantas palomas en palomares y tenemos más palomas que palomares, entonces en (al menos) un palomar habrá más de una paloma.

Un ejemplo sencillo de aplicación de este principio:

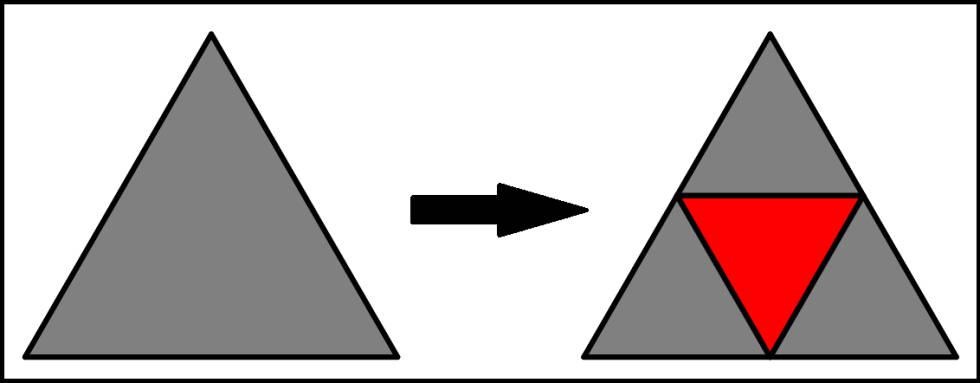
Si consideremos un triángulo equilátero de 2 m de lado y dibujamos 5 puntos dentro de él, siempre ocurrirá que al menos dos de esos puntos distarán entre sí menos de 1 m.

Es evidente que los cinco puntos dibujados son las palomas. Por otro lado, si unimos los puntos medios de los lados del triángulo equilátero considerado, se obtienen otros cuatro triángulos equiláteros, de 1 m de lado, que serían los palomares. Como hay más palomas que palomares, al menos dos de los cinco puntos estarán dentro de uno de los triángulos pequeños, es decir, a menos de 1 metro de distancia, uno del otro.

<Fuente: https://elpais.com/elpais/2017/01/10/el_aleph/1484088947_059937.html>

A una fiesta acuden 25 personas, chicos y chicas. Marta baila con 6 chicos; Rosa, con 7; Amanda, con 8, y así todas las chicas, hasta Lola, que baila con todos los chicos. ¿Cuántos chicos y cuántas chicas asisten a la fiesta?