El segundo teorema de Tales de Mileto dice que todo ángulo inscrito en una semicircunferencia es recto: 

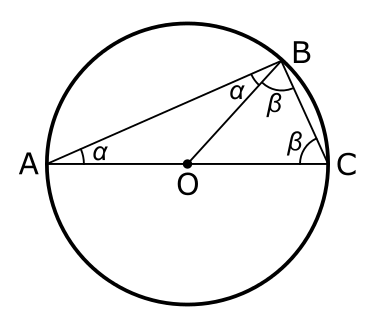
Dado que 2α + 2β = 180º, α + β = 90º

Por qué las funciones exponenciales del tipo   son las únicas que coinciden con sus derivadas

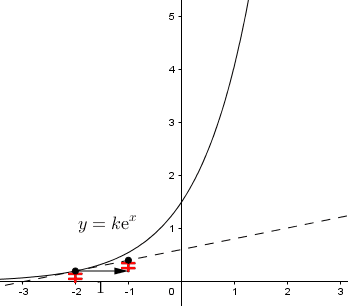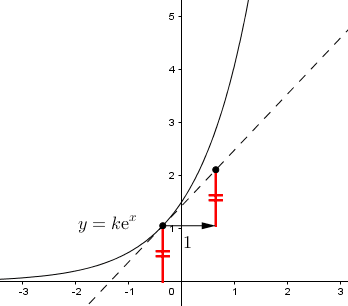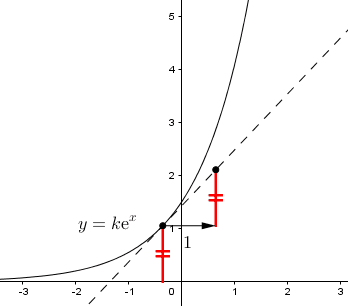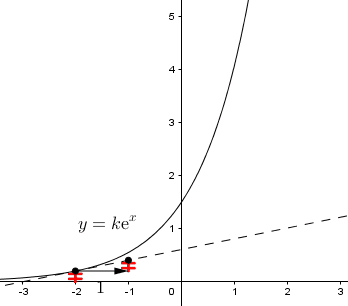
Veamos:

a) Si es de la forma, , entonces su función derivada es . Por tanto, . 

b) Recíprocamente, si es igual a su derivada, 

Multiplicamos la relación   por  : 

Reescribimos esta igualdad de la siguiente forma: 

Como  = , integrando en , tenemos , siendo   una constante.

Al pasar la exponencial del otro lado, finalmente obtenemos  

<Fuente: https://blogdemaths.wordpress.com/2017/12/03/fonctions-egales-a-leur-derivee>

Todos, en alguna ocasión, hemos tenido que luchar con un remolino de pelo que no hemos podido domar, ya sea en nuestra propia cabeza o en la cabeza de alguien cuyo cabello hemos intentado domesticar. Pues la existencia de dichos remolinos, aunque pueda parecer increíble, tiene explicación matemática. 

Vamos a imaginar una pelota (una esfera tridimensional) llena de pelo, con un pelo en cada punto de la superficie de la misma. Al “peinar” dicha pelota lo que hacemos es, básicamente, colocar cada pelo de forma tangente a la propia pelota. Algo así como lo que puede verse en esta imagen (las flechas serían los pelos):

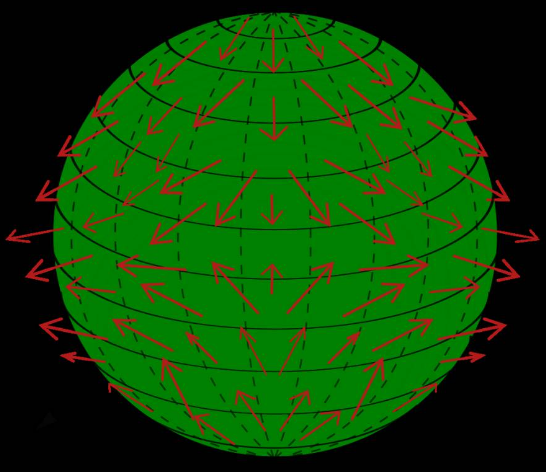
Esta disposición de vectores tangentes a cada punto de la superficie de la pelota se llama campo de vectores tangentes a la esfera. Como nuestro objetivo es “peinar” la pelota completa, necesitaríamos que en todos los puntos el vector tangente (el pelo) fuera como una de esas flechitas. O, dicho de manera informal, que “el pelo saliera hacia afuera”. En términos de vectores, necesitaríamos que el vector tangente a cada punto de la superficie de la esfera fuera distinto del vector cero.

Pues bien, el teorema de la bola peluda dice que todo campo de vectores tangentes sobre la esfera tiene al menos un cero. Es decir, peinemos como peinemos (usemos el campo de vectores tangentes que usemos) siempre habrá al menos un punto en el que nos toparemos con un remolino (un vector tangente nulo).

Si llevamos esto a nuestra cabeza, y suponiéndola esférica (no lo es, pero nos sirve) y con un pelo en cada punto de su superficie (de acuerdo, en realidad no es así, pero para el caso nos vale), nunca podremos peinarla de forma perfecta, siempre nos encontraremos algún remolino que, irremediablemente, no podremos “arreglar”.

Como en muchas otras ocasiones, uno podría pensar que el teorema de la bola peluda es otro resultado matemático más sin importancia y sin aplicaciones prácticas. El propio teorema (como todos) tiene ya interés e importancia matemática, pero además nos ayuda a explicar un fenómeno meteorológico.

Tomemos el planeta Tierra como una esfera (vale, ésta tampoco es una esfera perfecta, pero nos vuelve a servir) y el viento en cada punto de la misma como campo de vectores tangentes. Por el teorema de la bola peluda, habrá al menos un punto de la superficie de nuestro planeta en que el vector tangente será el vector cero. Ese vector cero es una especie de huequecito, alrededor del cual tendríamos el remolino. 

El teorema de la bola peluda es la explicación matemática de por qué en todo momento hay al menos un ciclón en la superficie de la Tierra. Y, dependiendo de cómo sople el viento (es decir, dependiendo del campo de vectores tangentes que tengamos), en un cierto instante podría haber más de uno (el teorema dice “al menos uno”, pero no nos da ni un número exacto ni un número máximo).

<Artículo completo: https://elpais.com/elpais/2017/12/05/el_aleph/1512493714_003529.html>

Dos cuerdas, AB y AC, de una circunferencia se cortan en un punto P, interior a ella. Demuestra que AP · PB =CP · PD.  Demuestra también que las medidas de esos cuatro segmentos no pueden ser cuatro números consecutivos.

<http://www.matematicasjmmm.com/new-blog-1/2017/12/4/geometra-124-secantes>