El príncipe de Toscana preguntó un dia a Galileo: "¿Por qué cuando se lanzan tres dados, obtenemos con más frecuencia la suma 10 que la suma 9, aunque ambas se puedan obtener de seis maneras diferentes cada una?"
9 = 1+2+6 = 1+3+5 = 1+4+4 = 2+2+5 = 2+3+4 = 3+3+3
10 = 1+3+6 = 1+4+5 = 2+2+6 = 2+4+4 = 2+3+5 = 3+3+4
Fue éste uno de los problemas más discutidos de su época. Galileo lo resolvió demostrando que los seis sucesos no son equiprobables. El juego presenta 6^3 = 216 resultados posibles y equiprobables, de los cuales 25 son favorables al suceso "suma = 9" y 27 al suceso "suma = 10". En efecto:
1+2+6, 1+3+5 y 2+3+4 representan cada uno 3! = 6 resultados; 1+4+4 y 2+2+5 representan cada uno 3 resultados, y 3+3+3, sólo uno. En total, 25 resultados favorables a "suma = 9".
1+3+6, 1+4+5 y 2+3+5 representan cada uno 6 resultados; 2+2+6, 2+4+4 y 3+3+4 representan cada uno 3 resultados. En total, 27 resultados favorables a "suma = 10"
Por tanto:
Probabilidad ("suma=9") = 25/216 = 0'116 y Probabilidad ("suma=10") = 27/216 = 0'125.
La diferencia es muy pequeña y sólo se puede comprobar experimentalmente realizando una exhaustiva prueba.

Una teselación es poligonal no regular, cuando se tesela el plano con figuras que se obtienen de un polígono regular, cortando o añadiendo en uno de sus lados algún tipo de figura y repitiéndola en el lado opuesto mediante deslizamientos, giros o reflexiones.
Muchos artistas han utilizado teselaciones en su trabajo. El holandés M.C. Escher es probablemente el más famoso de todos ellos. Se "divirtió" teselando el plano con siluetas de pájaros, peces y otros animales.
Los únicos polígonos regulares que pavimentan una superficie plana son los triángulos equiláteros, los cuadrados y los hexágonos regulares.





> Muerte: una célula viva morirá si en su entorno hay menos de dos células vivas o más de tres.
> Supervivencia: una célula viva permanecerá en ese estado si en su entorno hay dos o tres células vivas.
> Nacimiento: una célula muerta nacerá si en su entorno hay, exactamente, tres células vivas.



En los aleros de los tejados de los templos sintoístas y budistas, los fieles colgaban tablillas de madera, como ofrendas, con exquisitos dibujos que hacían gala del refinamiento artístico que había alcanzado por entonces el arte japonés. Entre estas tablillas había algunas con figuras geométricas, (triángulos, circunferencias, elipses o esferas), planteando fascinantes problemas matemáticos. Eran los sangaku, que literalmente quería decir “tablilla matemática”.
En la tablilla se incluía la respuesta, pero no la manera de resolver el problema. Luego, esta tablilla se mecía al viento en el alero de alguna casa o templo planteando su reto silencioso: ¡Resuélveme si puedes!
Parece probable que algunos maestros utilizaran este tipo de problemas en la enseñanza de las Matemáticas en las escuelas, pero todo apunta a que se trataba de Matemáticas puramente recreativas y que eran practicadas por campesinos, comerciantes o samuráis por el puro placer de resolver un problema.
Actualmente se han llegado a recuperar y clasificar 825 sangaku que estaban repartidos por entre casi todas las prefecturas de Japón. La mayoría de ellos se pueden resolver utilizando los conocimientos de la geometría euclidiana que se imparten en los primeros cursos de enseñanza media. Pero algunos son extremadamente difíciles y requieren técnicas matemáticas modernas, como el cálculo o el empleo de transformaciones afines. A pesar de que la finalidad de los sangaku es meramente recreativa, en ellos aparecen algunos teoremas importantes de la Matemática occidental.
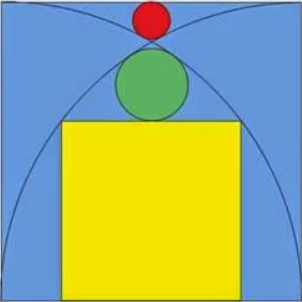
Un ejemplo sencillo de sangaku es el siguiente:
Partimos de un cuadrado de lado conocido, el cuadrado azul de la imagen. ¿Cuánto miden los radios de las circunferencias roja y verde y el lado del cuadrado amarillo?
Página 64 de 93