
El problema de los 100 prisioneros fue planteado por Anna Gál y Peter Bro Miltersen, dos investigadores daneses en 2003 y se puede enunciar como sigue:
Tenemos a 100 prisioneros y cada uno de ellos tiene un número distinto (del 1 al 100) en su gorro, que ellos pueden ver perfectamente, basta con que se quiten el gorro. En un habitación de la prisión tenemos 100 casilleros, también numerados del 1 al 100, y dentro de cada cajón hemos puesto una tarjeta con un número del 1 al 100 que, lógicamente, no tiene por qué coincidir con el del cajón en cuestión. El alcaide de la prisión es un poco sádico y les propone jugar para decidir si se salvan todos o mueren todos. Para ello, cada prisionero, por separado, entrará en la habitación del casillero, y puede abrir como máximo 50 cajones para encontrar aquel en el que está la tarjeta con el número de su gorro. Antes de salir, vuelve a cerrar todas los cajones. Si, siguiendo estas reglas, todos encuentran su número, se salvan todos. En otro caso, si un prisionero no encuentra su número en las 50 cajones que abre, morirán todos.

¿Con qué probabilidad se salvan todos si abren los 50 cajones a lo loco, sin pensar? Vamos a calcularla, que no es complicado. Para ello pensemos en el primer prisionero: si abre aleatoriamente 50 de los 100 cajones, la mitad, la probabilidad de que encuentre su número es de eso, la mitad, ½.
Como son 100 prisioneros, la probabilidad de que todos encontraran su número en estas condiciones sería:
![]()
Vamos, que se mueren todos con probabilidad casi del 100%. La crueldad del alcaide es así, qué le vamos a hacer. Bueno, sí que podemos hacer algo. En situaciones desesperadas hay que tomar decisiones desesperadas y en este caso se trata solamente de pensar un poco.
Los prisioneros puede decidir una estrategia común, al fin y al cabo todos quieren que los demás acierten su número. Y la estrategia es tan simple como la siguiente. El prisionero k (el que lleva una k en su gorro y lo sabe) abre primero el cajón k si está su número, ha ganado; en otro caso, abre el cajón cuyo número ha encontrado en la cajón k. Si está el suyo ha ganado, en otro caso, abre el cajón que indica este segundo número encontrado y así hasta que encuentre el suyo o hasta que haya abierto 50 cajones.
Veamos un ejemplo con 8 prisioneros:

En este ejemplo se salvarían todos. El prisionero 1 abre el cajón 1, después la 3, después la 6 y ahí está su número. Con el resto de prisioneros ocurre lo mismo, encuentra su número antes de abrir 4 cajones
¿Qué pasaría en la siguiente situación?

En este caso solo los prisioneros 4, 6 y 8 encontrarían su número con la estrategia y, por lo tanto, morirían todos.
¿Qué diferencia hay entre los dos ejemplos? Vamos a representar ambas situaciones mediante un grafo, donde los vértices serán los 8 números y las aristas (flechas) indicarán el recorrido que hace un prisionero por los cajones.
Así, el grafo del primer ejemplo sería el siguiente:

En esta distribución se forman ciclos, caminos circulares de vértices, que son de longitud 3 como máximo. Por lo tanto, ningún prisionero dará más de 3 pasos y no abrirá más de 3 cajones. Porque cualquier camino que empiece en el cajón cuyo número coincide con su gorro regresa a dicho número después de, como máximo, 3 pasos. En el caso del 5 y el 8 solo necesitan 2 pasos.
Sin embargo en el segundo ejemplo, el grafo quedaría así:

En este caso, según el ciclo en rojo, por ejemplo el prisionero 7 encontraría la tarjeta del 1 en el cajón 7, abriría el cajón 1 y encontraría el 2; abriría el 2 y encontraría el 3; y abriría el 3, y no puede abrir más, y se encuentra el 5. Todos muertos.
Bueno, esto nos da una pista para calcular la probabilidad de que se salven todos en el caso de 100 prisioneros: la probabilidad de que se salven es la probabilidad de que al hacer la distribución de tarjetas el alcaide, en el grafo dirigido asociado no haya ningún ciclo de longitud mayor que 50. Y esa probabilidad es del 0,31183. Dicho de otra manera, la probabilidad de salvarse con la estrategia de abrir los cajones según la tarjeta que contengan es, nada más y nada menos, del 31,18%. Alucinante, ¿no? Recuerda que sin estrategia la probabilidad de salvarse es prácticamente cero.
¿Y no se puede mejorar? Pues no. Se ha demostrado que la estrategia descrita es la estrategia óptima. Además, se sabe que si el número de prisioneros tiende a infinito, la probabilidad de que se salven tiende a 30'68%. Es decir, por muchos prisioneros que haya, esta estrategia garantiza la salvación de todos con una probabilidad superior al 30%.
<Artículo completo: http://www.abc.es/ciencia/abci-dilema-cien-prisioneros-201705161136_noticia.html>
Problema planteado en la XIV Olimpiada Provincial de Matemáticas para alumnos de 4º de ESO en Valladolid, en el año 2006:
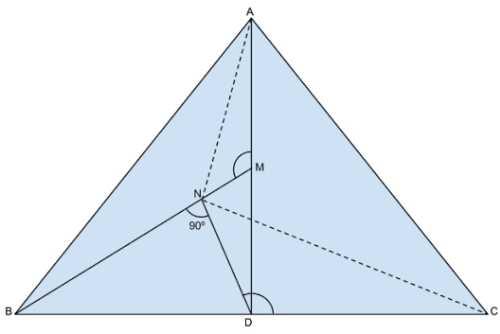
Sea ABC un triángulo isósceles con AB = AC. Sea D el punto medio del lado BC, M el punto medio del segmento AD y N el pie de la perpendicular trazada desde D sobre BM. Demuestra que el ángulo ANC = 90º.
Supongamos que una persona quiere construir un almacén en una determinada comarca, para poder distribuir diariamente un cierto tipo de producto a tres pueblos de la zona . Por limitaciones de carga, no puede transportar la mercancía desde el almacén haciendo menos de tres viajes; es decir, tiene que hacer un viaje a cada pueblo. ¿Dónde le conviene construir la nave para que el número de kilómetros recorridos sea el menor posible?
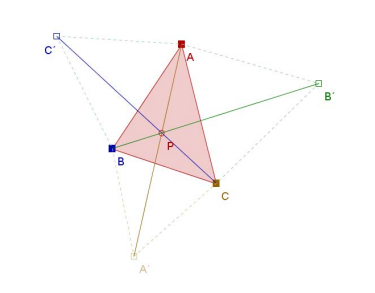
Esta situación tiene que ver con un problema de optimización propuesto por Pierre Fermat (1601-1665) y que dice lo siguiente:
Se considera un triángulo ABC y un punto P interior. Consideramos la suma de las longitudes de los segmentos trazados desde el punto a los tres vértices. Se trata de encontrar el punto P para el cual la suma anterior es mínima. (Dicho punto se conoce con el nombre de punto de Fermat del triángulo)
Se construyen tres triángulos equiláteros sobre los lados de ABC y hacia el exterior de éste: ABC´, BCA´ y ACB´. El punto buscado P es la intersección de las tres rectas AA´, BB´ y CC´: https://goo.gl/3aiBuj
Un camino hamiltoniano sobre un grafo es un camino, o sucesión de aristas adyacentes, que visita todos los vértices del grafo una sola vez. Si, además, el último vértice visitado es adyacente al primero, el camino recibe el nombre de ciclo hamiltoniano; (en este caso, se podría optar por finalizar el recorrido en el punto de partida, y así completar el ciclo).
Los caminos y ciclos hamiltonianos surgen después de que William Rowan Hamilton propusiera, a modo de juego, encontrar un ciclo hamiltoniano sobre el grafo de un dodecaedro.
El problema de encontrar un ciclo (o camino) hamiltoniano sobre un grafo arbitrario no es, en general, un problema sencillo.
<Solución: https://youtu.be/epmUQ4573z4>
Página 63 de 93

