
Seguro que recordáis aquella escena de Los Simpson donde Homer se sentaba muy serio delante de su hijo y le decía: Hijo, si de verdad quieres algo en esta vida, vas a tener que trabajar muy duro por ello. Ahora, cállate, que van a dar el número de la lotería en la tele...
¿Cómo es de probable que a nuestro amigo Homer le toque el premio gordo de la lotería de Navidad? La siguiente simulación nos acerca a la respuesta.
La Teoría de Juegos es una rama de las matemáticas cuyo objetivo es el estudio del comportamiento de los jugadores, sabiendo que la estrategia de cada jugador depende de las estrategias que realicen los demás. Se utiliza en economía, sociología, biología, politología, estrategia militar...
- "Si confiesas el delito cometido y tu compañero también confiesa, pasarás 6 años en prisión."
- "Si callas y tu compañero también calla, pasarás 6 meses en prisión
- "Si tu callas y tu compañero confiesa, pasarás 10 años prisión"
- "Si tu confiesas y tu compañero calla, saldrás libre".
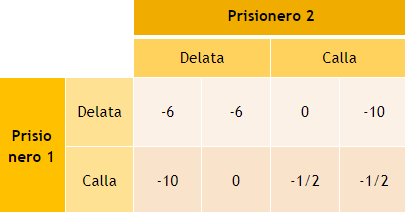
- Si el Prisionero 1 Delata y el Prisionero 2 Delata, obtendrán cada uno 6 años de prisión (-6, -6). pagos negativos lógicamente.
- Si el Prisionero 1 Calla y el Prisionero 2 Delata, habrá 10 años de prisión para el Prisionero 1 y 0 años de prisión para el Prisionero 2. (-10, 0).
- Si los dos callan, 1/2 año de prisión para cada uno (-1/2,-1/2)
- Si el Prisionero 2 Calla y el Prisionero 2 Delata, (0, -10)
- ¿Qué me pasará si el Prisionero 2 Delata? (Columna 1) Pues si yo Delato, me paso 6 años de cárcel y si Callo me paso 10 años de cárcel. Prefiero Delatar.
- Qué me pasará si el Prisionero 2 Calla? (Columna 2) Pues si yo Delato tengo 0 años de cárcel y si Callo tengo 1 año de cárcel. Prefiero Delatar.
- ¿Qué me pasará si el Prisionero 1 Delata? (Fila 1) Pues si yo Delato, me paso 6 años de cárcel y si Callo me paso 10 años de cárcel. Prefiero Delatar.
- Qué me pasará si el Prisionero 1 Calla? (Fila 2) Pues si yo Delato tengo 0 años de cárcel y si Callo tengo 1 año de cárcel. Prefiero Delatar.
- Los puntos de Equilibrio de Nash son aquellos que los jugadores han elegido como mejor respuesta.
- En el equilibrio de Nash ningún jugador puede arrepentirse de la estrategia que ha adoptado y, sin embargo, el resultado puede no ser tan bueno como el que se obtendría en una situación de cooperación.
- El equilibrio de Nash no tiene que ser siempre la mejor opción. En el Dilema del Prisionero la mejor opción es Calla-Calla.
Si Pedro es más alto que Juan, y Juan es más alto que Luis, está claro que Pedro también es más alto que Luis. Sin embargo, si Pedro es amigo de Juan, y Juan es amigo de Luis, Pedro no tiene por qué ser amigo de Luis. Esta propiedad de las relaciones entre ciertos elementos se denomina en matemáticas propiedad transitiva, y, como acabamos de ver, puede cumplirse o no dependiendo del tipo de elementos que comparemos y de la relación que queramos establecer entre ellos.
Vamos a plantear un juego con dados. Pero no con unos dados “habituales”, de los de siempre, sino con unos dados muy particulares. Son estos tres:
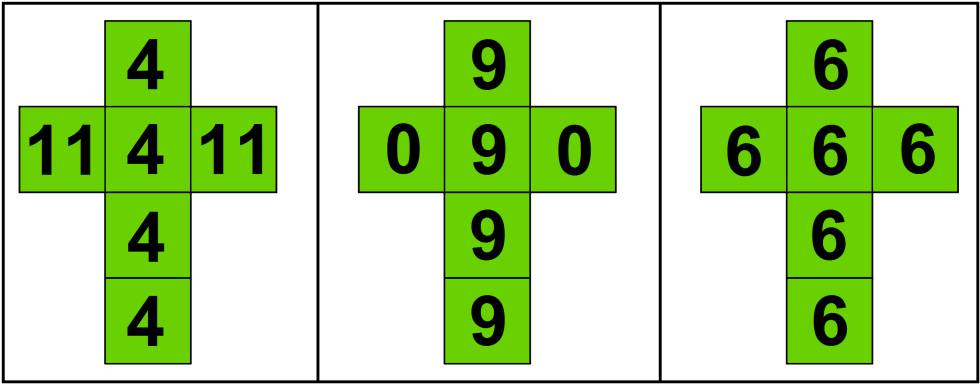
La idea es que elijáis uno de los dados para jugar contra mí, que elegiré otro después (os dejo elegir primero, mira que soy bueno…). Cuando hayamos elegido, tiramos los dos dados y anotamos la puntuación obtenida en cada uno. Si en cada tirada gana la mayor puntuación, y vosotros queréis ganarme, ¿qué dado elegiríais para jugar? Esto es, ¿qué dado os proporcionaría una mayor probabilidad de ganarme?
Vamos a analizar las probabilidades de cada uno de los tres enfrentamientos para ver cuál os convendría elegir para jugar.
Comparemos primeros el primer dado de la izquierda, llamémosle dado A, con el del centro, que será el dado B. Aquí tenéis una tabla con todos los posibles resultados, en la que he coloreado de azul los casos en los que gana el dado A y en verde los casos en los que gana el dado B:
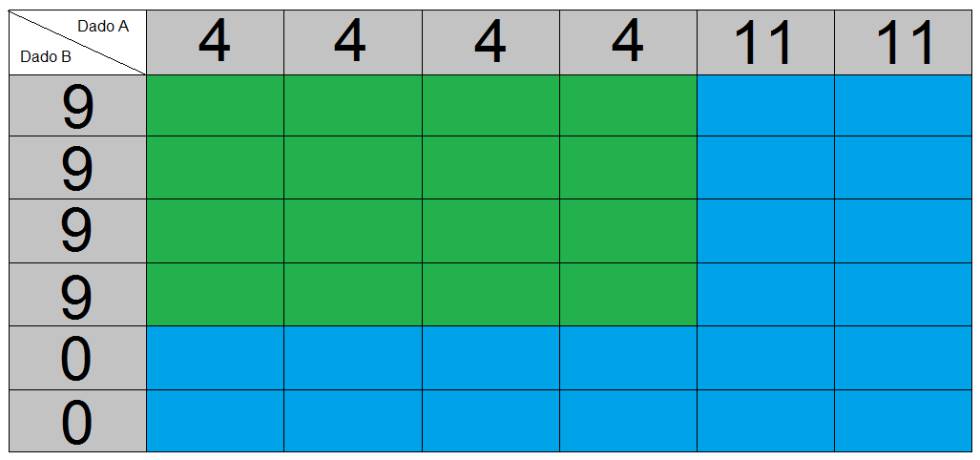
Como podéis ver, el dado A gana más veces que el B, 20 a 16. Por tanto, no os interesa elegir el dado B, porque en ese caso yo elegiría el dado A y, a la larga, os acabaría ganando (la probabilidad de que yo gane sería mayor).
Ahora comparemos el B con el de la derecha, que llamaremos dado C. En la siguiente tabla podéis ver cómo quedaría la cosa (B en verde y C en morado):
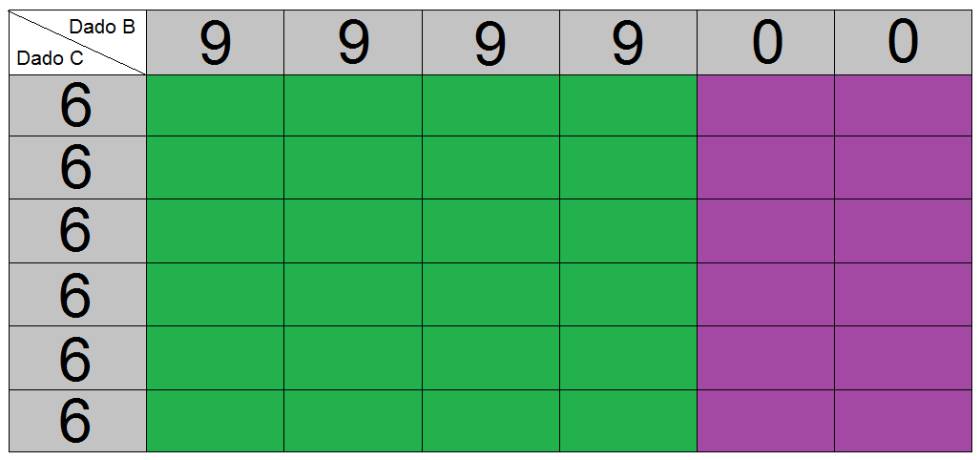
En este caso, vemos que el dado B gana más veces que el C, 24 a 12. Esto significa que tampoco os interesa elegir el C, ya que yo elegiría el B y tendría mayor probabilidad de ganaros.
Bien, la cosa parece clara: si no os interesa elegir el B (porque pierde con el A) ni el C (porque pierde con el B), entonces conviene que elijáis el A, ¿verdad? Sí, sí, elegid el A…y yo elegiré el C:
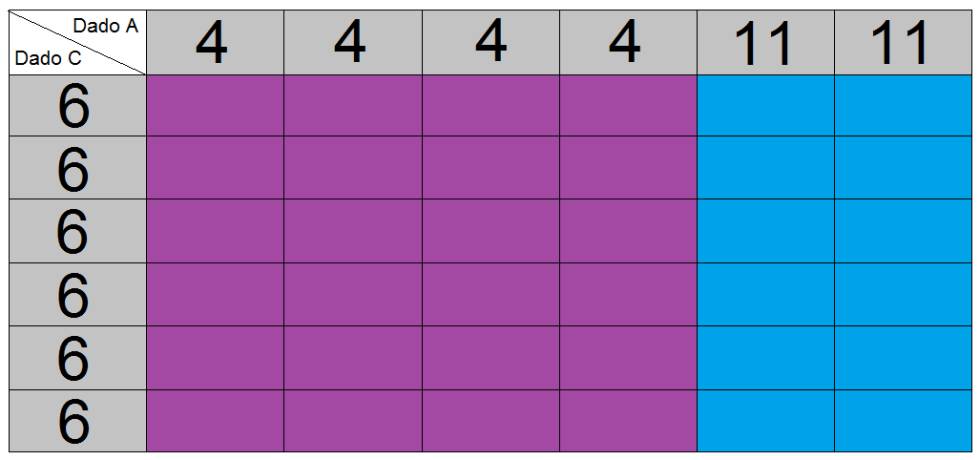
Como se puede ver en la tabla, el dado C gana más veces que el A, de nuevo 24 a 12.
Tenemos entonces que el dado A gana al dado B, el dado B gana al dado C y el dado C gana al dado A. Esto significa que elijáis el dado que elijáis, lo más probable es que siempre gane yo, ya que siempre podré elegir un dado con mayor probabilidad de ganar que el vuestro (quizás en realidad no sea tan bueno dejándoos elegir primero…).
Estos dados tan traviesos se denominan dados no transitivos, porque, como acabamos de ver, no cumplen la propiedad transitiva (si A gana a B y B gana a C, entonces A debería ganar a C, pero hemos visto que no es así). Este ejemplo no es ni mucho menos el único, existen mucho juegos de tres dados no transitivos…y también con cuatro dados, y con cinco, y general se pueden construir ciclos con el número de dados queramos donde el primero gana al segundo, el segundo al tercero, y así sucesivamente hasta el último, que gana al primero.
Una última curiosidad sobre estos dados. Imaginaos que ahora cada uno tiene que tirar su dado dos veces y sumar la puntuación. ¿Qué dado elegiríais ahora? Pensad, que también os dejo elegir primero…
En este caso también estáis perdidos, si elegís primero la probabilidad de que yo gane sigue siendo mayor que la vuestra. Lo curioso es que las ventajas entre los dados se invierten. Es decir, en este nuevo juego el dado B gana al dado A, el dado C gana al dado B y el dado A gana al dado C. Os invito a que creéis vosotros unas tablas parecidas a las que os he mostrado en este artículo para esta modalidad del juego y que veáis así claramente esta inversión de ventajas.
<Artículo completo: https://elpais.com/elpais/2017/06/21/el_aleph/1498064711_481863.html>
Al inicio del juego están todos los espacios ocupados excepto uno. El jugador debe mover una pieza cada vez y las piezas sólo pueden moverse capturando mediante un salto sobre otra, como en las damas. Sólo se pueden capturar las piezas en horizontal o en vertical y nunca en diagonal.
El objetivo del juego es eliminar todas las piezas dejando sólo una en el tablero. En la animación adjunta se ve como se resuelve el juego con éxito en un determinado tablero:
<Para jugar puedes visitar https://goo.gl/prZZdh o https://goo.gl/aSVEkH>
Descripción del juego
En la versión más tradicional del juego, se utilizan tres varillas verticales. En una de ellas, se apila un cierto número de discos, ordenados de mayor a menor tamaño, y el objetivo consiste en pasar todos los discos de dicha varilla a una de las otras dos, ayudándose de la tercera, siguiendo dos simples reglas:
1.- Sólo se puede mover un disco de cada vez, y ha de ser el más pequeño.
2.- Nunca un disco puede descansar sobre otro de menor tamaño.
Leyenda
En el gran templo de Benarés, bajo la cúpula que señala el Centro del Mundo, reposa una bandeja de cobre en la que están plantadas tres agujas de diámetro más fino que el aguijón de una abeja. En el momento de la Creación, Dios colocó en una de las agujas 64 discos de oro puro, ordenados por tamaño: desde el mayor, que reposa sobre la bandeja, hasta el más pequeño, en lo más alto del montón. Incansablemente, día tras día, los sacerdotes del Templo mueven los discos haciéndolos pasar de una aguja a otra de acuerdo con leyes fijas e inmutables que dictan que el sacerdote en ejercicio no mueva más de un disco a la vez ni lo sitúe encima de un disco de menor tamaño. El día en que los 64 discos hayan sido trasladados desde la aguja en que Dios los puso al crear el mundo a una cualquiera de las otras dos agujas, ese día el Templo y, con gran estruendo, el mundo, desaparecerán.
No obstante, esta leyenda resultó ser un invento publicitario del creador del juego, el matemático Éduard Lucas. En aquella época, era muy común encontrar matemáticos ganándose la vida de forma itinerante con juegos de su invención, de la misma forma que los juglares hacían con su música. La falacia resultó ser tan efectista y tan bonita, que ha perdurado hasta nuestros días.
Una pregunta razonable podría ser: Si la leyenda fuese realidad y se lograse pasar todos los discos, ¿cuándo llegaría el fin del mundo?
El mínimo número de movimientos que se necesita para resolver este problema es de 264-1 Si los monjes hicieran un movimiento por segundo, los 64 discos estarían en la otra varilla en algo menos de 585 mil millones de años. Como comparación para ver la magnitud de esta cifra, la Tierra tiene como 5 mil millones de años, y el Universo entre 15 y 20 mil millones de años de antigüedad, sólo una pequeña fracción de esa cifra.
<Para jugar puedes visitar http://www.novelgames.com/es/tower>
Página 61 de 93


