Si Pedro es más alto que Juan, y Juan es más alto que Luis, está claro que Pedro también es más alto que Luis. Sin embargo, si Pedro es amigo de Juan, y Juan es amigo de Luis, Pedro no tiene por qué ser amigo de Luis. Esta propiedad de las relaciones entre ciertos elementos se denomina en matemáticas propiedad transitiva, y, como acabamos de ver, puede cumplirse o no dependiendo del tipo de elementos que comparemos y de la relación que queramos establecer entre ellos.
Vamos a plantear un juego con dados. Pero no con unos dados “habituales”, de los de siempre, sino con unos dados muy particulares. Son estos tres:
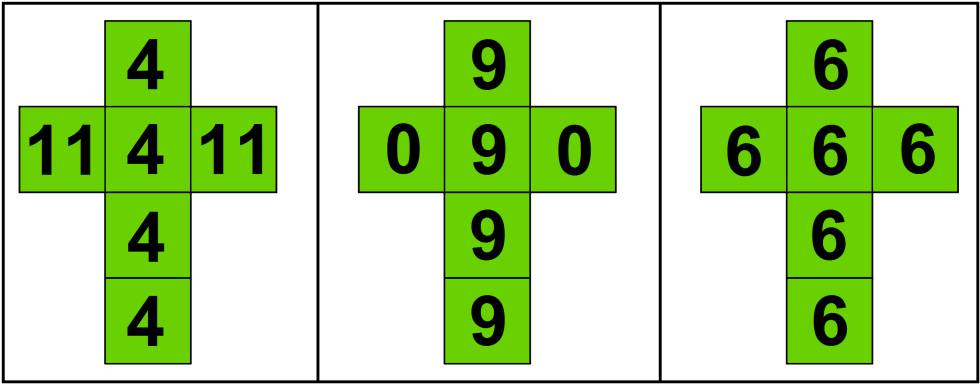
La idea es que elijáis uno de los dados para jugar contra mí, que elegiré otro después (os dejo elegir primero, mira que soy bueno…). Cuando hayamos elegido, tiramos los dos dados y anotamos la puntuación obtenida en cada uno. Si en cada tirada gana la mayor puntuación, y vosotros queréis ganarme, ¿qué dado elegiríais para jugar? Esto es, ¿qué dado os proporcionaría una mayor probabilidad de ganarme?
Vamos a analizar las probabilidades de cada uno de los tres enfrentamientos para ver cuál os convendría elegir para jugar.
Comparemos primeros el primer dado de la izquierda, llamémosle dado A, con el del centro, que será el dado B. Aquí tenéis una tabla con todos los posibles resultados, en la que he coloreado de azul los casos en los que gana el dado A y en verde los casos en los que gana el dado B:
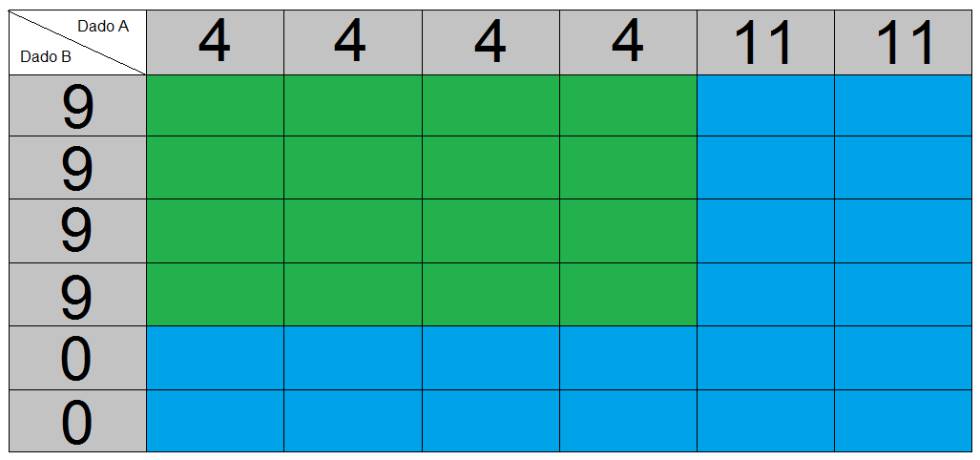
Como podéis ver, el dado A gana más veces que el B, 20 a 16. Por tanto, no os interesa elegir el dado B, porque en ese caso yo elegiría el dado A y, a la larga, os acabaría ganando (la probabilidad de que yo gane sería mayor).
Ahora comparemos el B con el de la derecha, que llamaremos dado C. En la siguiente tabla podéis ver cómo quedaría la cosa (B en verde y C en morado):
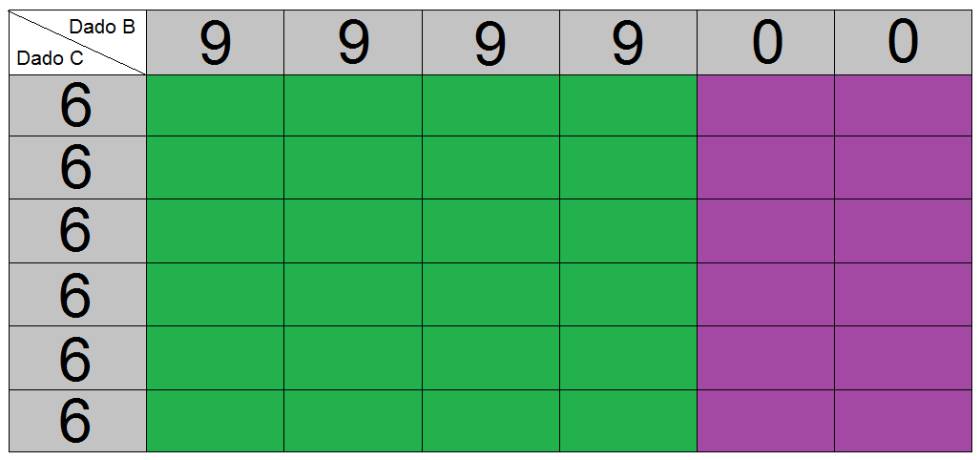
En este caso, vemos que el dado B gana más veces que el C, 24 a 12. Esto significa que tampoco os interesa elegir el C, ya que yo elegiría el B y tendría mayor probabilidad de ganaros.
Bien, la cosa parece clara: si no os interesa elegir el B (porque pierde con el A) ni el C (porque pierde con el B), entonces conviene que elijáis el A, ¿verdad? Sí, sí, elegid el A…y yo elegiré el C:
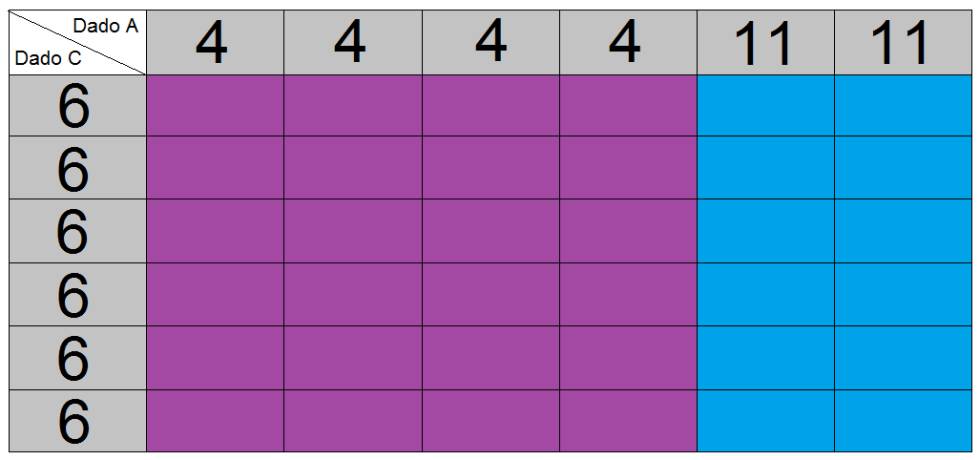
Como se puede ver en la tabla, el dado C gana más veces que el A, de nuevo 24 a 12.
Tenemos entonces que el dado A gana al dado B, el dado B gana al dado C y el dado C gana al dado A. Esto significa que elijáis el dado que elijáis, lo más probable es que siempre gane yo, ya que siempre podré elegir un dado con mayor probabilidad de ganar que el vuestro (quizás en realidad no sea tan bueno dejándoos elegir primero…).
Estos dados tan traviesos se denominan dados no transitivos, porque, como acabamos de ver, no cumplen la propiedad transitiva (si A gana a B y B gana a C, entonces A debería ganar a C, pero hemos visto que no es así). Este ejemplo no es ni mucho menos el único, existen mucho juegos de tres dados no transitivos…y también con cuatro dados, y con cinco, y general se pueden construir ciclos con el número de dados queramos donde el primero gana al segundo, el segundo al tercero, y así sucesivamente hasta el último, que gana al primero.
Una última curiosidad sobre estos dados. Imaginaos que ahora cada uno tiene que tirar su dado dos veces y sumar la puntuación. ¿Qué dado elegiríais ahora? Pensad, que también os dejo elegir primero…
En este caso también estáis perdidos, si elegís primero la probabilidad de que yo gane sigue siendo mayor que la vuestra. Lo curioso es que las ventajas entre los dados se invierten. Es decir, en este nuevo juego el dado B gana al dado A, el dado C gana al dado B y el dado A gana al dado C. Os invito a que creéis vosotros unas tablas parecidas a las que os he mostrado en este artículo para esta modalidad del juego y que veáis así claramente esta inversión de ventajas.
<Artículo completo: https://elpais.com/elpais/2017/06/21/el_aleph/1498064711_481863.html>


