El Juego del Drago, inventado por los matemáticos John Horton Conway y Michael Stewart Patterson en la década de los 60 del siglo XX, es un juego para dos jugadores. Comienza con una cierta cantidad de puntos dispuestos de la forma que queramos, cuantos más puntos más largo será el juego y mayor complejidad tendrá. Esos puntos se llaman brotes, y la mecánica del juego es que, de manera alternativa, cada jugador una con una línea, llamada rama (no necesariamente recta, vale una curva), dos de esos brotes o un brote consigo mismo y, después, añada un nuevo brote encima de la línea que acaba de dibujar.

Por ejemplo, comenzando con tres brotes podríamos unir dos como muestra la figura siguiente, y añadir entonces un nuevo brote sobre dicha línea (el de color verde):

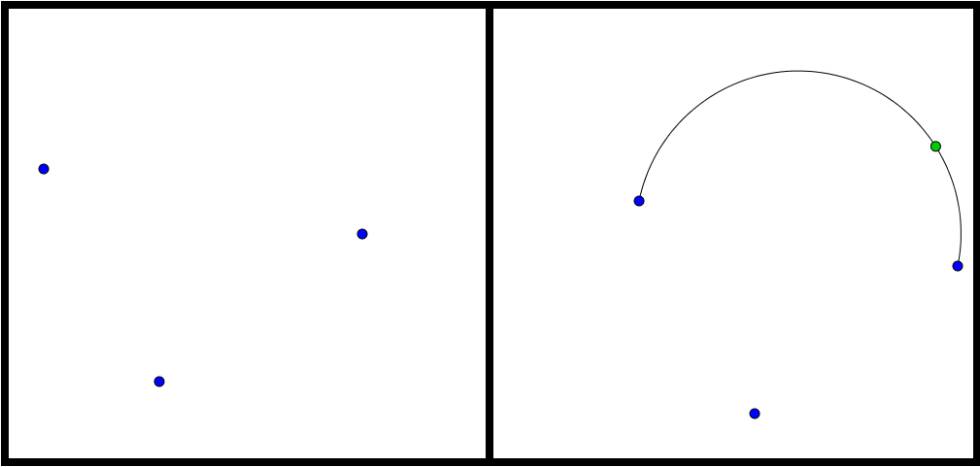
Pero no podemos añadir líneas a nuestro antojo, sino que debemos seguir tres reglas:

1.- La rama (que, como hemos dicho, no tiene por qué ser recta) no puede cortarse a sí misma ni tampoco a otra rama que ya estuviera dibujada.

2.- Una rama no puede pasar por otros brotes que no sean los dos que queremos unir.

3.- No pueden salir más de tres ramas de ningún brote.

Cuando de un brote sale exactamente tres ramas, se dice que el brote está muerto, y por tanto ya no podrá usarse para dibujar una nueva rama.

Llegará un momento en el que ya no se puedan dibujar más líneas, ya sea porque todos los brotes han muerto, porque al dibujar una línea superemos las tres ramas en un cierto brote, porque las únicas ramas que podamos añadir corten a alguna que ya está dibujada…En ese caso, en la versión habitual del juego, gana el jugador que haya añadido la última rama.

Una posible partida del Juego del Drago comenzando con tres brotes:

Y ya no se pueden hacer más movimientos, ya que los únicos brotes que todavía sobreviven son los que aparecen en rojo en la siguiente imagen pero no se pueden unir sin cortar a una rama que ya esté dibujada (incumpliríamos la primera regla):

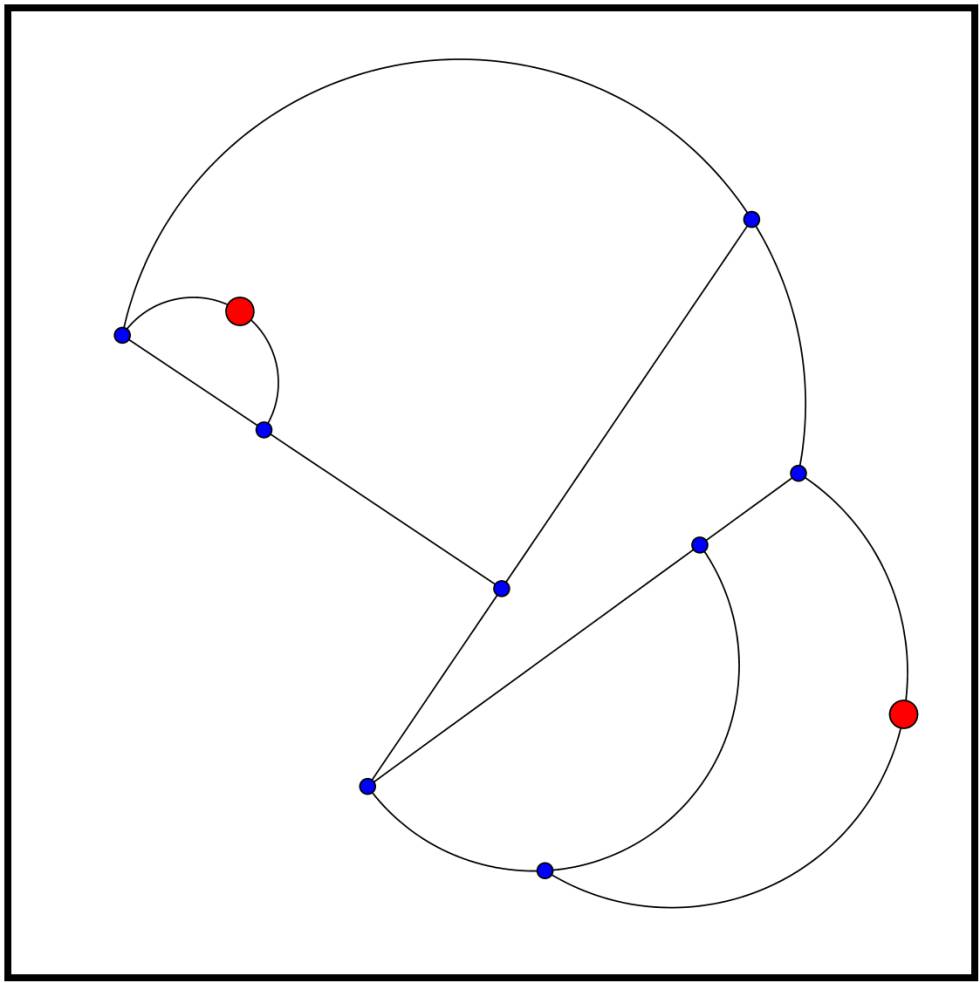
Tampoco podemos añadir una rama que una uno de esos dos brotes consigo mismo, ya que entonces tendríamos un brote del que salen cuatro ramas, incumpliendo así la tercera regla.

Como suele ser habitual en estos juegos, se ha estudiado matemáticamente el juego del drago en lo que a finalización y estrategias se refiere. La primera cuestión que es interesante plantearse es si todas las partidas terminarán. Teniendo en cuenta que en cada movimiento aumenta el número de brotes, podría ser que alguna partida pudiera alargarse indefinidamente… Pero eso es imposible en este juego. De hecho, está demostrado que, si se comienza con N brotes, el número de turnos es, como mucho, 3N-1. Es decir, todas las partidas del juego del drago terminan. Por dar otro dato, también se sabe que, como mínimo, cada partida tendrá 2N turnos.

Y, por otro lado, está la cuestión de las posibles estrategias que pueden seguir los jugadores con el objetivo de ganar una partida. La cuestión es que, al ser un juego que acaba en un número finito de pasos y en el cual no se puede empatar, el juego del drago tiene estrategia ganadora para alguno de los dos jugadores. Otra cosa es encontrar dicha estrategia…

La cuestión es que, actualmente, se sabe para qué jugador hay estrategia ganadora en unos cuantos casos, que dependen del número inicial de brotes. Por ejemplo, con 2 brotes hay estrategia para que gane el segundo jugador; para 3, 4, y 5 brotes iniciales la hay para que sea el primer jugador el que resulte ganador; para 6, 7 y 8 brotes el segundo jugador tiene estrategia ganadora; para 9, 10 y 11 la tiene el primero…

¿Veis algún patrón? Parece que sí, ¿verdad? Tranquilos, no os emocionéis todavía. Cierto es que parece que la posesión de estrategia ganadora sigue un patrón en función del número inicial de brotes, pero, por desgracia, en la actualidad es solamente una conjetura. Más concretamente, es esta conjetura:

“Conjetura del juego del drago: Existe estrategia ganadora para el primer jugador si el número inicial de brotes deja resto 3, 4 ó 5 al dividirlo entre 6; en otro caso, existe estrategia ganadora para el segundo jugador.”

A día de hoy se conoce (está demostrado) para qué jugador hay estrategia ganadora para todos los números iniciales de brotes hasta 44, y también para 46, 47 ó 53, y todos esos casos cuadran con la conjetura anterior. Pero todavía no se sabe si la conjetura resultará ser cierta o si, por el contrario, algún valor del número inicial de brotes incumplirá la misma.

<Artículo completo: https://elpais.com/elpais/2017/12/14/el_aleph/1513264299_865763.html>