
Consideremos los cuatro primeros números naturales: 1, 2, 3, y 4. Elijamos al azar dos de ellos, a y b, y realicemos la siguiente operación: a+b+a.b. Tomemos este resultado y los dos números restantes, (es decir, c, d y a+b+a.b), y repitamos la operación anterior. Con el nuevo resultado y el número aún no elegido, volvemos a realizar de nuevo el cálculo. Llegamos así a un resultado que, independientemente de los números elegidos en cada momento, siempre será el 119.

Veamos algunos casos:
Caso I
Comenzamos con {1, 2, 3, 4}. Cogemos, por ejemplo, el 2 y el 4: 2 + 4 + 2·4= 14
Tenemos ahora el conjunto {1, 3, 14}. Cogemos el 1 y el 3: 1 + 3 + 1·3= 7
Llegamos al conjunto de dos números {7,14}. Obtenemos finalmente 7 + 14 + 7·14= 119.
Caso II
Volvamos a {1, 2, 3, 4}. Cogemos ahora el 1 y el 4: 1 + 4 + 1·4= 9.
En el conjunto {2, 3, 9} cogemos el 3 y el 9: 3 + 9 + 3·9= 39.
Llegamos al conjunto {2, 39} y otra vez resulta 2 + 39 + 2·39= 119.
Caso III
De {1, 2, 3, 4} cogemos el 2 y el 3: 2 + 3 + 2·3= 11.
De {1, 4, 11} cogemos 1 y 11: 1 + 11 + 1·11= 23
En {4, 23} operamos y resulta: 4 + 23 + 4·23= 119.
Si alguien cree que es puro azar, puede probar los 12 casos posibles y así convencerse de que siempre aparece el 119. Pero, ¿por qué se llega siempre a este resultado?
<Visto en http://matematicasnarua.blogspot.com.es/2012/08/para-quen-lle-gusten-os-numeros.html>
Para ir de A a B, una hormiga iba a veces por el camino azul, otras por el verde y otras por el atajo rojo. Es obvio que los caminos azul y verde tienen la misma longitud porque ACBD es un rectángulo... pero también el camino rojo tiene esa misma longitud... ¡Un falso atajo! ¿Cuál es entonces la razón entre los lados del rectángulo?

<Visto en http://joselorlop.blogspot.com.es/2018/01/697-falso-atajo-resolucion.html>
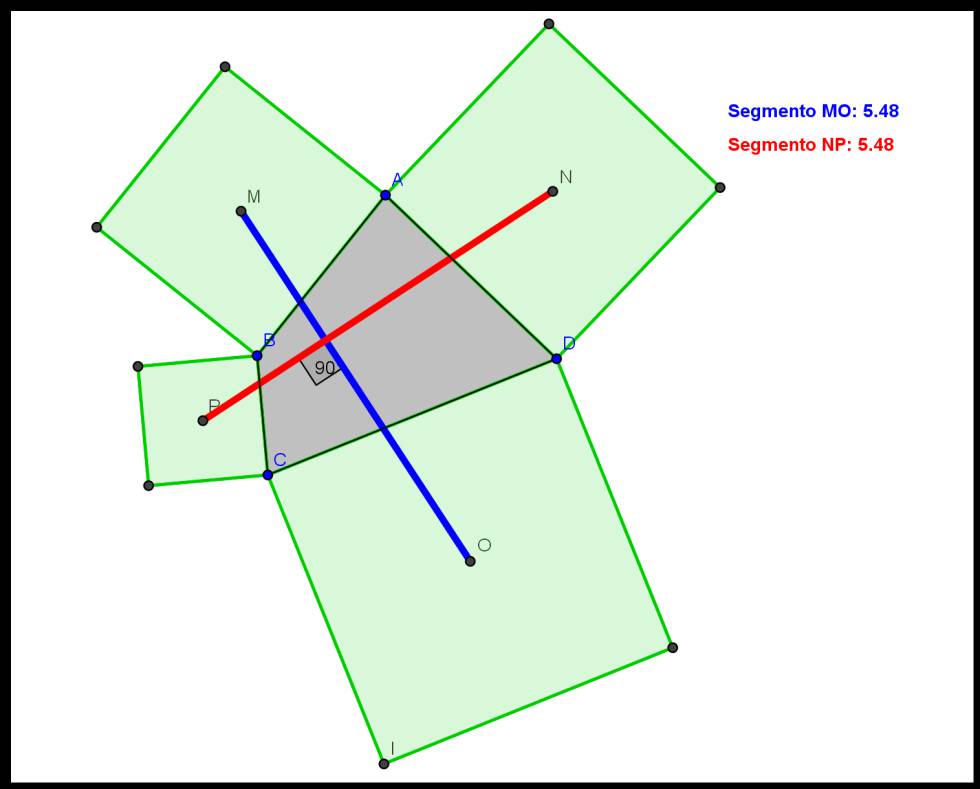
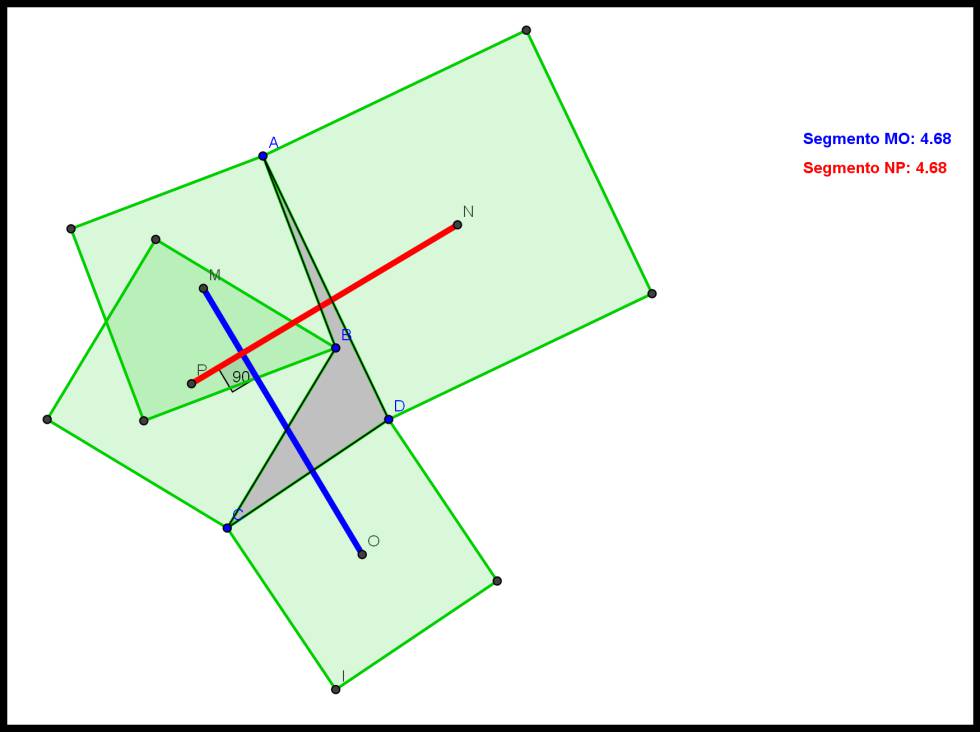
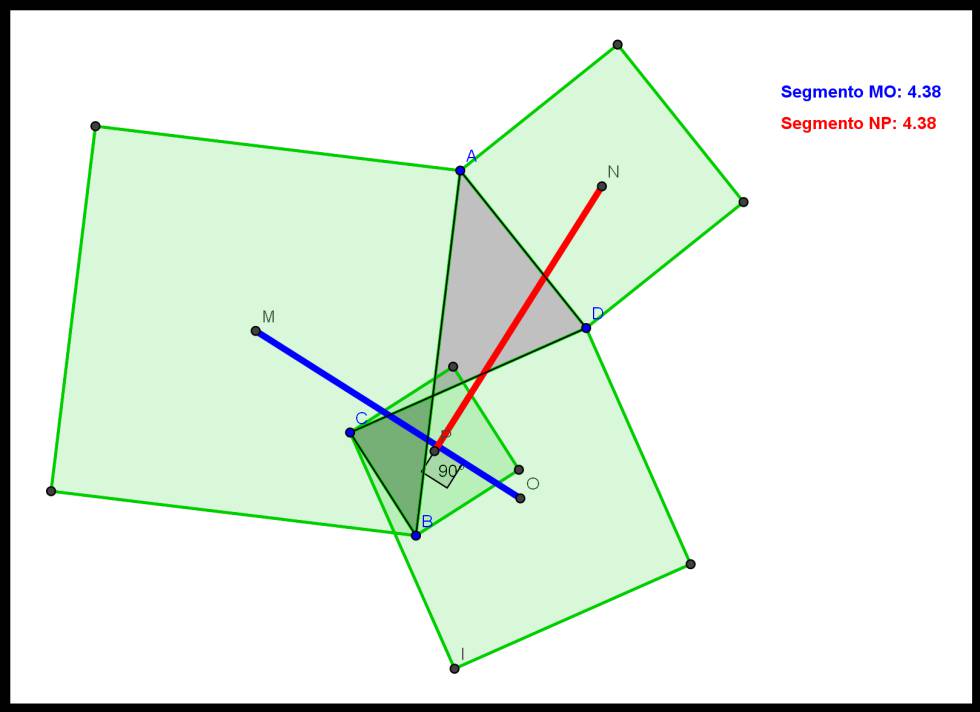
Consideremos un cuadrilátero cualquiera en el plano. Si adosamos cuadrados a cada uno de sus lados, los segmentos que unen los centros de cuadrados opuestos tienen la misma longitud y además son perpendiculares.
Lo más sorprendente de este teorema es que, como puede leerse en el enunciado, es válido para cualquier cuadrilátero. Se cumple para cuadriláteros convexos:
Pero también se cumple para cuadriláteros no convexos:
E, incluso, para cuadriláteros en los que hay intersecciones entre sus lados:
<Artículo completo: https://elpais.com/elpais/2018/01/10/el_aleph/1515599296_007426.html>
Destaca por su simplicidad, puesto que manipula símbolos sobre una tira de cinta siguiendo una serie de reglas, pero la MÁQUINA DE TURING ha servido de base para el desarrollo teórico en las ciencias de la computación y en la teoría de la complejidad.
“Después de ser secuestrado, te despiertas en una gran sala donde vemos 1.000 bombillas apagadas, numeradas del 1 al 1.000. Notas que te estás quedando sin oxígeno, por lo que necesitas salir de esa habitación. Al fondo ves una puerta. Intentas abrirla, pero no hay manera, es imposible, está bloqueada…
En ese momento, una voz grave sale de algún lugar de la habitación y dice lo siguiente:
‘Imagine que pudiera encender y apagar cada una de las bombillas que hay en la habitación. En esa hipotética situación, comenzando con la bombilla 1 y siguiendo un orden ascendente, colóquese mentalmente delante de cada bombilla y cambie de estado todas las que tengan un número que sea múltiplo de la bombilla en la que está situado en ese instante.
Tras llegar a la bombilla 1.000 y realizar dicha operación con ella, ¿qué bombillas terminarán encendidas? Piénselo bien, de su respuesta depende que salga de la habitación o que permanezca ahí para siempre. Si da con la respuesta correcta, recuperará su libertad. Tiene un minuto para dar con ella.’
¿Conseguiríais salir de la habitación o, por el contrario, vuestra vida terminaría en aquel lugar? Analizad el problema y pensadlo durante un rato mientras aclaro algunos detalles:
- Cambiar de estado una bombilla es encenderla si estaba apagada o apagarla si estaba encendida.
- No puedes volver atrás, es decir, primero haces lo que te dicen en la bombilla 1, luego en la 2, después en la 3, y así sucesivamente en orden ascendente.
- Un número es múltiplo de sí mismo.

Piensa el problema con menos bombillas, 10 por ejemplo. Vamos paso a paso haciendo lo que nos han ordenado:
- Bombilla 1: encendemos las bombillas 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10.
- Bombilla 2: apagamos las bombillas, 2, 4, 6, 8, y 10.
- Bombilla 3: apagamos la 3, encendemos la 6 y apagamos la 9.
- Bombilla 4: encendemos la 4 y la 8.
- Bombilla 5: apagamos la 5 y encendemos la 10.
- Bombilla 6: apagamos la 6.
- Bombilla 7: apagamos la 7.
- Bombilla 8: apagamos la 8.
- Bombilla 9: encendemos la 9.
- Bombilla 10: apagamos la 10.
Después de todo esto, quedan encendidas las bombillas 1, 4 y 9. Uhmmm…
<Artículo completo: https://elpais.com/elpais/2018/01/04/el_aleph/1515079619_023957.html>
Página 58 de 93
