El Juego de la vida, creado por el matemático británico John Horton Conwayen en el año 1970, está referido a una cuadrícula infinita. En ella habitan ciertos organismos elementales o células que, de forma individual, ocupan algunas de las muchas celdas que la constituyen.
Con el paso del tiempo, unas células mueren, otras sobreviven, pero también aparecen otras nuevas. Las reglas son muy sencillas. Cada vez que transcurre una unidad de tiempo, su "mundo" evoluciona de acuerdo con los siguientes principios:
> Muerte: una célula viva morirá si en su entorno hay menos de dos células vivas o más de tres.
> Supervivencia: una célula viva permanecerá en ese estado si en su entorno hay dos o tres células vivas.
> Nacimiento: una célula muerta nacerá si en su entorno hay, exactamente, tres células vivas.
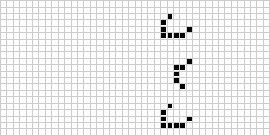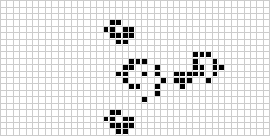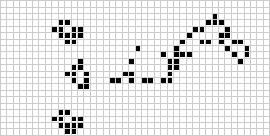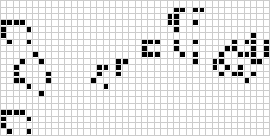
Vamos a ver un ejemplo. En nuestro espacio, hemos pintado de morado las células vivas:

Si nos fijamos en la célula A1, como en su entorno solo hay una célula viva, en la siguiente etapa A1 morirá; la célula A2, en cambio, nacerá, puesto que tiene 3 células vivas (moradas) en su entorno; las cĺulas A3, A4, A5 y B1, se quedan iguales porque ninguna de ellas tiene exactamente 3 células vivas en su entorno; la B2, morirá por tener más de 3 células vivas en su entorno... y así, sucesivamente.
En la siguiente etapa, tendríamos esta configuración:

Si siguen jugando con este ejemplo, comprobarán que tras cuatro etapas llegan a la configuración inicial pero que se ha desplazado en el espacio.

Exiten configuraciones estáticas como "el bloque" o "el barco", y otras recurrentes como "el oscilador" o "el planeador" (patrones que se repiten con giro o traslación).
Podemos encontrar también configuraciones que se estabilizan después de un cierto tiempo. Si lo hacen después de muchos turnos o generaciones se llaman "Matusalenes". Un ejemplo de este tipo de configuración es el patrón "Diehard" que desaparece después de 130 turnos, mientras que el patrón "Acorn" tarda 5206 turnos en estabilizarse en forma de muchos osciladores, y en ese tiempo genera 13 planeadores.
Lo sorprendente del juego de la vida es que un conjunto de reglas tan sencillas baste para generar patrones tan interesantes. Configuraciones sencillas, como los planeadores, nos recuerdan los aminoácidos, las moléculas orgánicas básicas a partir de las cuales se construye la vida.
Una de las aplicaciones prácticas es servir como base para simulaciones físicas a partir de unas reglas o premisas extremadamente simples. Un ejemplo es el simulador de líquidos en dos dimensiones que permite ver algunas de sus posibilidades. Las reglas son muy parecidas a las del juego de la vida y hacen comportarse a los píxeles de distintos colores como átomos sobre los que actúan fuerzas como la presión y la gravedad.
También están las simulaciones de ciertos procesos químicos o incluso biológicos, tales como la formación de los patrones en la piel, el pelo o las conchas de ciertos animales. En las plantas sucede otro tanto: el comportamiento de los estomas (células de la epidermis de las hojas) es relativamente fácil de simular con unas pocas reglas. Con algo más de complejidad se puede simular también el funcionamiento de las neuronas, creando modelos que pese a su simplicidad acaban mostrando una extraordinaria complejidad cuando se les aplican ciertos patrones o valores iniciales.
En el fondo, esa es la grandeza del comportamiento tanto del juego de la vida como de otros autómatas celulares: que de algo tan simple pueda surgir algo tan elaborado y complejo.
Así que... entra en el Juego de la vida a través de cualquiera de estos dos simuladores, Game of Life, de Edwin Martin y JavaScript Game of Life de Pedrovam), y experimenta por ti mismo.
<Fuentes: https://goo.gl/8V6Z7W y https://goo.gl/73tRqX>


