Supongamos que una persona quiere construir un almacén en una determinada comarca, para poder distribuir diariamente un cierto tipo de producto a tres pueblos de la zona . Por limitaciones de carga, no puede transportar la mercancía desde el almacén haciendo menos de tres viajes; es decir, tiene que hacer un viaje a cada pueblo. ¿Dónde le conviene construir la nave para que el número de kilómetros recorridos sea el menor posible?
Esta situación tiene que ver con un problema de optimización propuesto por Pierre Fermat (1601-1665) y que dice lo siguiente:
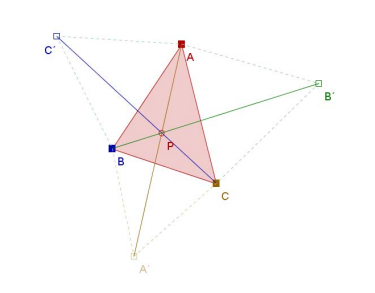
Se considera un triángulo ABC y un punto P interior. Consideramos la suma de las longitudes de los segmentos trazados desde el punto a los tres vértices. Se trata de encontrar el punto P para el cual la suma anterior es mínima. (Dicho punto se conoce con el nombre de punto de Fermat del triángulo)
Se construyen tres triángulos equiláteros sobre los lados de ABC y hacia el exterior de éste: ABC´, BCA´ y ACB´. El punto buscado P es la intersección de las tres rectas AA´, BB´ y CC´: https://goo.gl/3aiBuj