Las funciones exponenciales y sus derivadas

Por qué las funciones exponenciales del tipo $f (x) = k \ times \ text {e} ^ {x}$ son las únicas que coinciden con sus derivadas

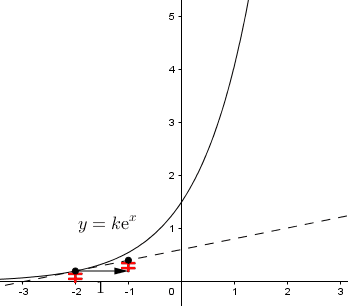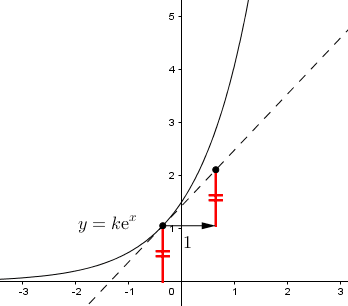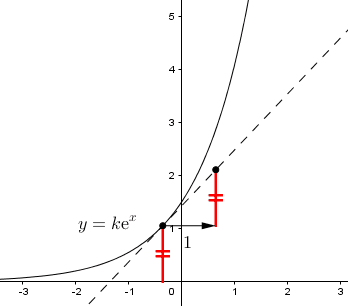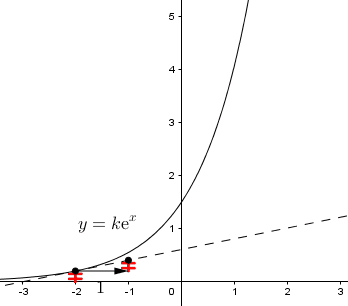
Veamos:

a) Si $F$ es de la forma, $x \ mapsto k \ times \ text {e} ^ {x}$ , entonces su función derivada es $f '(x) = k \ times \ text {e} ^ {x}$ . Por tanto, $f (x) = f '(x)$ .

b) Recíprocamente, si $F$ es igual a su derivada, $f '(x) - f (x) = 0 \ quad \ quad (\ estrella \ estrella)$

Multiplicamos la relación $(\ estrella \ estrella)$ por $\ Texto {e} ^ {- x}$ : $f '(x) \ times \ text {e} ^ {- x} - f (x) \ times \ text {e} ^ {- x} = 0$

Reescribimos esta igualdad de la siguiente forma: $f '(x) \ times \ text {e} ^ {- x} + f (x) \ times \ left (- \ text {e} ^ {- x} \ right) = 0 \ quad \ quad (\ star \ star \ star)$

Como $u '\ times v + u \ times v'$ = $(u \ times v) '$ , integrando en $(\ estrella \ estrella \ estrella)$ , tenemos $f (x) \ times \ text {e} ^ {- x} = k$ , siendo $k$ una constante.