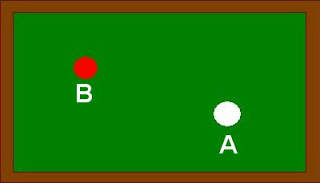
¿Qué trayecto debe recorrer la bola A para golpear a la bola B, después de rebotar en una, dos y tres bandas? Intenta visualizar el recorrido en cada caso, antes de ir a la solución.
- "Bieito, súmale tu nota al resultado de André, multiplica por 2, suma 1 y multiplica por 5. Pásale el resultado a Carlos".
- "Carlos, súmale tu nota al resultado de Bieito , multiplica por 2, suma 1 y multiplica por 5. Anuncia el resultado".

A: (2A+1).5=10A+5
B: [(B+10A+5).2 + 1].5 = 10B+100A +55
C: [(C+10B+100A+55).2 + 1].5 = 10C+100B+1000A+555
Si al resultado de C restamos 555 resulta 1000A+100B+10C; es decir, el número ABC0. En dicho número aparecen las notas de los tres alumnos.
Los conflictos entre seres racionales, que recelan uno del otro, o la pugna entre competidores que interactúan y se influyen mutuamente, siendo capaces de traicionarse entre sí, constituyen el campo de estudio de la Teoría de Juegos, la cual se basa en un análisis matemático riguroso que surge de manera natural al observar y analizar un conflicto desde un punto de vista racional.
Desde el enfoque de esta teoría, un “juego” es una situación conflictiva en la que priman intereses contrapuestos de individuos o instituciones. Y es en ese contexto que una de las partes, al tomar una decisión, influye sobre la decisión que tomarán las demás. Es decir, el resultado del conflicto se determina a partir de todas las decisiones tomadas por todos los participantes en dicho juego.
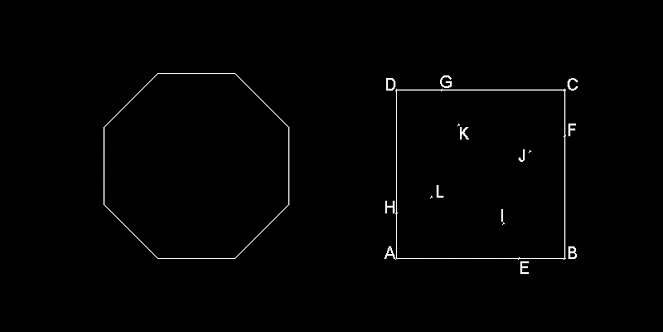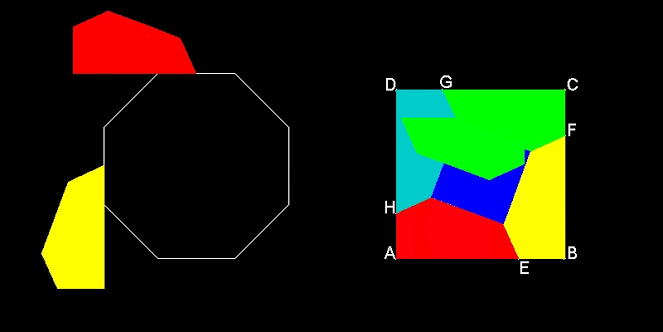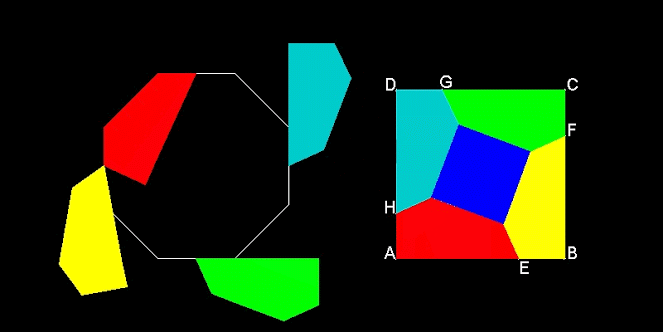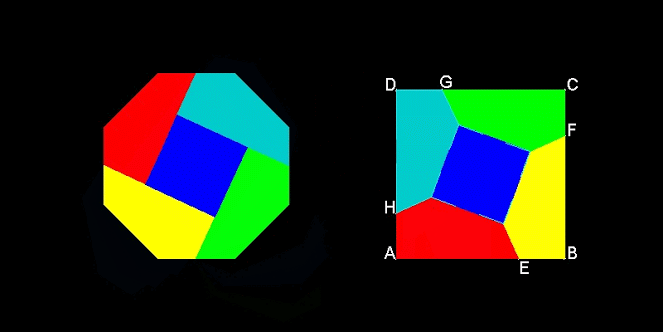
La descomposición de las figuras que muestra la siguiente imagen, nos dice cómo convertir un cuadrado en un octógono, sin variar su área:
¿Qué tienen en común James Bond, Superman y King Kong? Que necesitan las matemáticas para sus aventuras. El matemático y divulgador José María Sorando Muzás, catedrático de Educación Secundaria, realiza un recorrido sobre la relación de esta ciencia con el séptimo arte más allá de las películas de matemáticos. Esta grabación corresponde a la conferencia titulada "Matemáticas de cine", que forma parte del ciclo "Arte, Ciencia y Tecnología: miradas diferentes a una misma realidad". Está organizada por la Universidad Pública de Navarra en colaboración con la Fundación Española para la Ciencia y la Tecnología (FECYT)-Ministerio de Economía, Industria y Competitividad y el Planetario de Pamplona.
Página 70 de 93