La belleza de un edificio está en la mutua relación de todas sus partes y esa relación es armonía, proporción y canon, es decir, adecuación a una medida que gravita sobre el número. (San Agustín)
Hacia el año 1000, Ibn Al-Haytam escribió que la belleza es una propiedad divina fruto de la proporción y de la armonía. Dos características que podemos encontrar en la pequeña capilla de San Miguel de Celanova, en cuyo dintel figura la frase: «A ti, Dios, te creemos el autor de esta obra».
El investigador Roberto Vázquez Rozas, de la Universidad de Vigo, sostiene que esa afirmación sólo se puede entender si los promotores de esta joya siguieron con detalle las teorías estéticas de la época. Dice Vázquez que a Celanova llegó el conocimiento del Almagesto de Ptolomeo y la geometría de Euclides, que ya se conocían en la Córdoba del siglo X. Y tal sabiduría debió llegar, añade, «por algún especialista musulmán o de algún mozárabe andalusí»

<Artículo completo: http://www.lavozdegalicia.es/ocioycultura/2009/08/03/0003_7885408.htm>
El teorema de Ptolomeo afirma que si un cuadrilátero ABCD está inscrito en una circunferencia, entonces la suma de los productos de lados opuestos es igual al producto de las diagonales , es decir, AB. CD+ AD. BC=AC. BD.
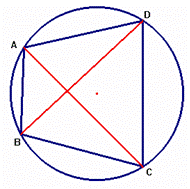
Existen multitud de demostraciones de este bello teorema. Aquí reproducimos la incluida en el libro Modern College Geometry, de David R. Davis, Addison-Wesley,1949:
Para realizar la demostración, se recurre a un punto auxiliar del segmento BD que llamaremos E, tal que el ángulo BAC es igual al ángulo DAE.

De acuerdo a esta construcción, se verifica que los triángulos DAE y ABC son semejantes. De donde:

Además, por ser también semejantes los triángulos BAE y CDA, se verifica:

De las dos igualdades, y del hecho que BE + ED = BD , obtenemos que AB.CD + BC.AD = AC.BD, que es lo queríamos demostrar.
Observación: si el cuadrilátero fuese un rectángulo, obtendríamos el teorema de Pitágoras. Es decir, el teorema de Pitágoras es un caso particular del teorema de Ptolomeo, o éste es una generalización de aquel.
<Fuente de la publicación: https://goo.gl/Y9UGEQ>
En combinatoria, los números de Catalan forman una secuencia de números naturales, (1, 2, 5, 14, 42, 132, 429, 1430, ...), que aparece en varios problemas de conteo de tipo recursivo. Obtienen su nombre del matemático belga Eugène Charles Catalan (1814–1894).
Consideremos, por ejemplo, una rejilla cuadrada de orden n. Pretendemos ir desde el vértice inferior izquierdo al superior derecho, moviéndonos sólo hacia la derecha y hacia arriba, y manteniéndonos en todo momento por debajo de la diagonal que une dichos vértices. ¿Cuántos caminos diferentes podemos elegir?
La respuesta nos la da el n-ésimo número de Catalan que se obtiene a partir de la fórmula que figura en la parte superior de la siguiente imagen:

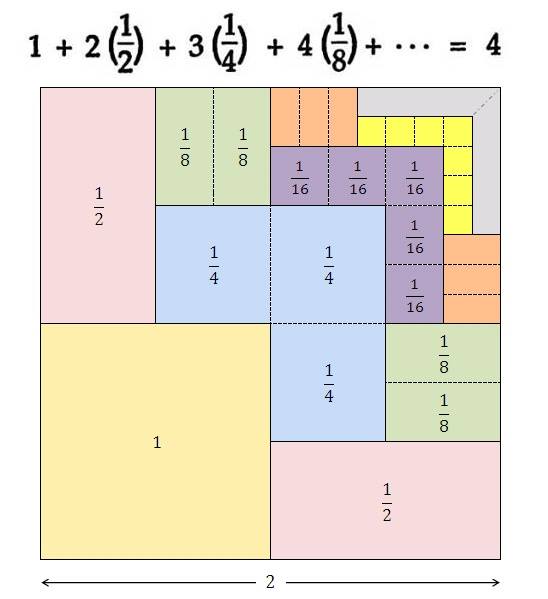
Uno de los conceptos de mayor dificultad es el concepto de infinito. Las construcciones recursivas de tipo fractal pueden ser de gran ayuda para una mejor comprensión de dicho concepto, especialmente cuando se trata de visualizar sumas de infinitos términos.

Página 75 de 93