
Hubo un tiempo, en la Italia del Renacimiento, en que sucedía algo difícil de pensar en nuestro tiempo: había desafíos públicos para ver quién resolvía mejor problemas de ecuaciones, con premios importantes, público ruidoso y abundante, y donde los jurados eran autoridades políticas destacadas.
Hubo varios de esos desafíos, pero aquí nos vamos a ocupar del más famoso de ellos: el que tuvo lugar en Milán el 10 de agosto de 1548 siendo los contendientes Nicolo Fontana (1499-1557), más conocido por el poco amable sobrenombre de ‘Tartaglia’, y Ludovico Ferrari (1522-65). El árbitro de mismo fue don Ferrante de Gonzaga, gobernador de Milán, que acudió junto con personalidades relevantes de la ciudad. Pero había un personaje ausente de forma voluntaria, que era el causante del desafío: Jerolamo Cardano (1501-76). Como se intuye un asunto complejo que intentaremos resumir y clarificar.
<Seguir leyendo en http://www.abc.es/ciencia/abci-genial-matematico-tartaja-lanzo-despecho-gran-desafio-algebraico-milan-201711131054_noticia.html>

Nicolo Fontana «Tartaglia»
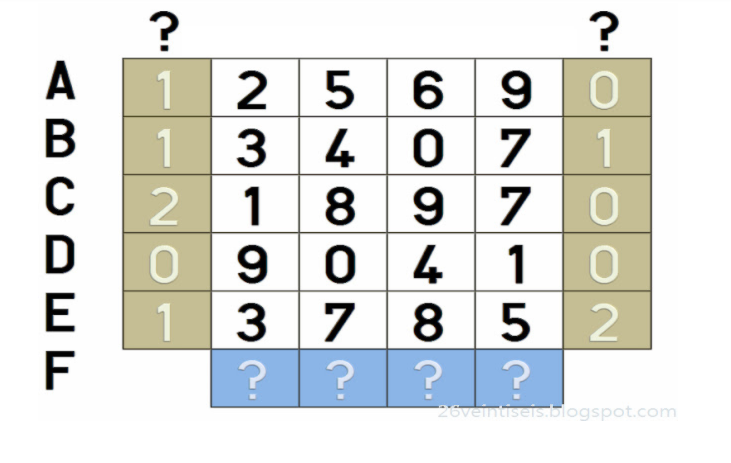
¿Qué número debe ir en la fila F de la siguiente tabla y de qué nos informan las columnas señaladas con una interrogación en su parte superior?
Del libro "Probabilidad y Estadística", de Arthur Engel: "Cada motor de un avión puede estropearse, con independencia de los otros, con una cierta probabilidad p. El avión se mantiene en vuelo si por lo menos funciona la mitad de los motores. ¿Qué avión es más seguro, el de 2 o el de 4 motores?"

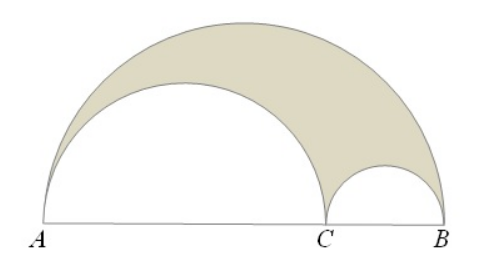
El árbelos, también conocido como la "cuchilla del zapatero", es la región comprendida entre dos semicircunferencias tangentes entre sí y una semicircunferencia tangente a ambas y de diámetro la suma de los diámetros de las primeras.

Escultura de un árbelos en Kaatsheuvel, Holanda
Arquímedes estudió originalmente dicha figura, fascinado por sus interesantes propiedades matemáticas. Destacamos dos de ellas:
i) La longitud del arco AC más la longitud del arco CB es igual a la longitud del arco AB.
ii) Si se construye una línea perpendicular desde C que corte al arco AB en un punto P, entonces PC es el diámetro de un círculo cuya área es igual a la del árbelos.
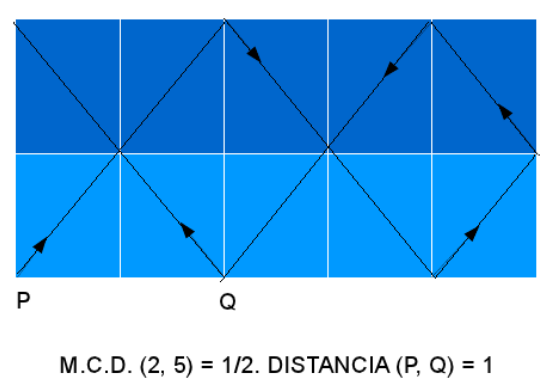
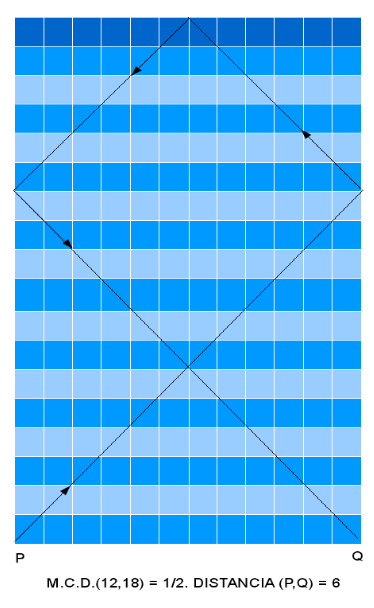
Consideremos un rectángulo de lados enteros. Si enviamos un rayo de luz a 45° partiendo del origen (vértice inferior izquierdo), el rayo, después de un número finito de “rebotes,” llegará seguro a otro de los vértices del rectángulo. En su recorrido, rebotará sobre la base en distintos puntos de la misma. La distancia del primero de dichos puntos, por la izquierda, al origen representa el doble del MÁXIMO COMÚN DIVISOR de los lados del rectángulo.
Página 79 de 93
