El teorema de Ptolomeo afirma que si un cuadrilátero ABCD está inscrito en una circunferencia, entonces la suma de los productos de lados opuestos es igual al producto de las diagonales , es decir, AB. CD+ AD. BC=AC. BD.
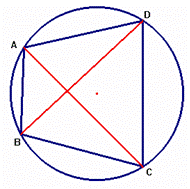
Existen multitud de demostraciones de este bello teorema. Aquí reproducimos la incluida en el libro Modern College Geometry, de David R. Davis, Addison-Wesley,1949:
Para realizar la demostración, se recurre a un punto auxiliar del segmento BD que llamaremos E, tal que el ángulo BAC es igual al ángulo DAE.

De acuerdo a esta construcción, se verifica que los triángulos DAE y ABC son semejantes. De donde:

Además, por ser también semejantes los triángulos BAE y CDA, se verifica:

De las dos igualdades, y del hecho que BE + ED = BD , obtenemos que AB.CD + BC.AD = AC.BD, que es lo queríamos demostrar.
Observación: si el cuadrilátero fuese un rectángulo, obtendríamos el teorema de Pitágoras. Es decir, el teorema de Pitágoras es un caso particular del teorema de Ptolomeo, o éste es una generalización de aquel.
<Fuente de la publicación: https://goo.gl/Y9UGEQ>


