Los número algebraicos son los números reales que son solución de alguna ecuación polinómica cuyos coeficientes son números racionales. A la vista de esta definición es fácil comprender que todos los números racionales son algebraicos, ya que si r=p/q es un número racional, entonces r es solución de la ecuación polinómica  q.x-p=0.

Pero no sólo son algebraicos los números racionales. También lo son muchos irracionales. Por ejemplo, el número irracional \sqrt{2} es algebraico. Basta ver que es solución de la ecuación polinómica x2-2=0 para darse cuenta de ello. Lo mismo ocurre con, por ejemplo, \sqrt[3]{3}, que es solución de x3-3=0. Y con muchos más números irracionales.

Los números trascendentes son los números reales que no son solución de ninguna ecuación polinómica de coeficientes racionales. Por lo que hemos visto antes todos los números trascendentes son irracionales, aunque no todos los irracionales son trascendentes. Como ejemplos más representativos de este conjunto numérico tenemos al número \pi y al número e.

 

 

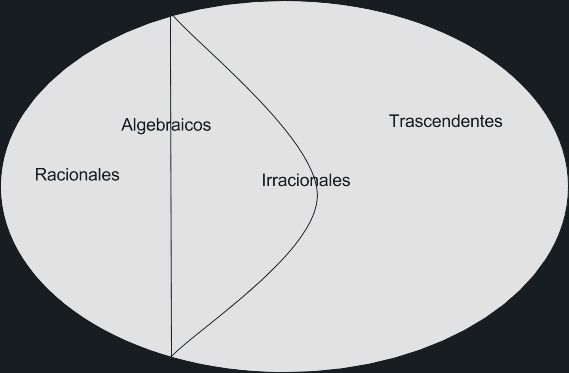
Viendo que en primera instancia es mucho más sencillo encontrar números algebraicos que números trascendentes uno podría pensar que hay muchos más del primer tipo que del segundo. Nada más lejos de la realidad. El conjunto de los números algebraicos es infinito numerable, es decir, tiene infinitos elementos pero podemos contarlos, mientras que el conjunto de los números trascendentes es infinito no numerable, esto es, también tiene infinitos elementos pero no los podemos contar. Conclusión: hay muchos más números reales trascendentes que algebraicos.

 

<Artículo completo en https://goo.gl/ejpLUJ>

 

Queremos encargar un depósito cilíndrico de 1000 decímetros cúbicos y colocarlo, de pared a pared, en una de las esquinas de un cuarto rectangular. Teniendo en cuenta que en dicha esquina hay un pilar con una parte visible de 15 cm de largo por 12 cm de ancho, ¿qué diámetro abarcará y qué altura alcanzará el depósito si, por razones de espacio, nos interesa que quede pegado al pilar?

   

https://www.desmos.com/calculator/kidv2y3uc9

 

Queremos duplicar el volumen de un cilindro sin variar su altura. ¿Por qué número hay que multiplicar el diámetro de su base? 

https://www.desmos.com/calculator/ex3siegru8

 

Consideremos un círculo de un cierto diámetro d rodando tangencialmente por el interior de otro círculo de diámetro 2d. ¿Qué lugar geométrico describirá un punto elegido sobre el círculo pequeño?

El ingeniero inglés Matthew Murray explotó este principio en 1802 para producir un motor hipocicloidal que transformase el movimiento lineal en movimiento circular.

 

https://www.desmos.com/calculator/bkaja5kl00

 

Hablando de los números primos una de las cosas que llama la atención es su caótica forma de aparecer. Al principio están muy próximos entre sí; por ejemplo, entre los primeros 20 números naturales contamos hasta 8 números primos, pero luego, entre el 83 y el 97 no encontramos ninguno.

Resultado de imagen de numeros primos

La pregunta que nos hacemos es: ¿podremos encontrar intervalos con 5, 10, 20, o incluso 1000, números compuestos consecutivos, es decir,  intervalos de cualquier tamaño sin números primos?
 
La respuesta es que sí, y la demostración es bastante sencilla. Por ejemplo, para conseguir un intervalo de 5 números consecutivos sin primos, basta con calcular 6!+k, con k=2, 3, 4, 5, 6: 
 
6·5·4·3·2·1+2 = 2.(6.5.4.3.1+1) = 722, que es múltiplo de 2
6·5·4·3·2·1+3 = 3.(6.5.4.2.1+1) = 723, que es múltiplo de 3
6·5·4·3·2·1+4 = 4.(6.5.3.2.1+1) = 724, que es múltiplo de 4
6·5·4·3·2·1+5 = 5.(6.4.3.2.1+1) = 725, que es múltiplo de 5
6·5·4·3·2·1+6 = 6.(5.4.3.2.1+1) = 726, que es múltiplo de 6
 
En general, para conseguir un intervalo de n números compuestos consecutivos, sin presencia de números primos, basta con calcular (n+1)!+k, con k=2, 3, ..., n.
 
Sin embargo, no hay un intervalo infinito de números compuestos consecutivos, sin primos, es decir,  el número de primos no es finito. Si hubiera un número finito de primos, el producto de todos ellos aumentado en 1 no sería divisible por ninguno de los números primos existentes y, en consecuencia, sería otro número primo. Dado que este razonamiento se puede continuar indefinidamente, la conclusión es que ¡el número de primos es infinito!
 
 
  1. La matriz inversa en el descifrado de mensajes
  2. Por fin se despejó la incógnita
  3. La danza de los factores
  4. El vagón de cola... controla
  • Está aquí:  
  • Inicio