Observa que si x es el número de bueyes e y el número de días que puede alimentarlos, x.y es la cantidad de raciones de pienso que tiene el campesino. 

Solución: https://goo.gl/Pv4488

Al decir de muchos, Marilyn vos Savant es la mujer más inteligente del mundo; en todo caso, durante añós figuró en el Libro Guinnes de los récords como la persona con el coeficiente de inteligencia más alto que jamás se haya medido, hasta que se suprimió esta sección del libro.

Esta señora publica una columna semanal (Ask Marilyn) en la revista estadounidense Parade (aquí su página Web, en inglés), en la que resuelve problemas de lógica y responde a preguntas de contenido filosófico. 

Un lector le planteó una vez la siguiente pregunta: «Si una gallina y media pone un huevo y medio en un día y medio, ¿cuántas gallinas hacen falta para que en seis días pongan seis huevos?»

La sabia mujer respondió: «A mi padre también le gustaba este problema, pero de niña logré entenderlo tan poco como hoy: ¿cuál es el problema? Si una gallina y media pone un huevo y medio, etc., significa que una gallina pone un huevo por día. Y si una única gallina pone cada día un huevo a lo largo de seis días, obtenemos exactamente seis huevos, ¿no es cierto?».

En este caso, Marilyn vos Savant se equivocó. La respuesta «una gallina» es incorrecta. Por lo que se ve, hasta los más sabios entre los sabios tienen problemas con el método de cálculo que nos enseñan en el colegio con el nombre de «regla de tres». 

<Artículo completo: http://lasmatematicas.eu/2017/10/04/matematicas-en-el-gallinero>

Solución ilustrada: https://goo.gl/zeRLfc

Le comunican a Grissom que se ha cometido un homicidio. Inmediatamente acude a la vieja fábrica abandonada donde se encuentra el cadáver, lo observa todo detenidamente y le pregunta al forense:

---“¿Hora de la muerte?”.

El médico responde:

---“La víctima parecía estar sana, por lo que podemos suponer que su temperatura corporal en el momento del suceso era de 36,5º. Cuando llegamos hace una hora la temperatura del cuerpo era 34º y ahora mismo es de 33º. Además la temperatura en el edificio es de 18º y parece que se mantiene bastante constante desde hace muchas horas. Con todos estos datos, podemos afirmar que la muerte ocurrió hace aproximadamente…”

Evidentemente, el médico no saca papel y boli y se pone a resolver ecuaciones diferenciales, sino que lo mira en una tabla de datos que contiene las posibles combinaciones.

Pero nosotros sí vamos a resolver esta ecuación:

Sea T(t) la temperatura del cuerpo en un cierto momento t, siendo t=0 el momento del asesinato. La ley de enfriamiento de Newton afirma que la rapidez con que se enfría un objeto es proporcional a la diferencia entre su temperatura y la temperatura del medio ambiente en el cual se encuentra dicho objeto. La ecuación que se plantea será entonces: T’(t)=k(18-T(t)), que resolviéndola nos da T(t) = 18 - ce^-kt, siendo c y k constantes a determinar, y t el instante considerado.

Como conocemos la temperatura del cuerpo en tres instantes distintos, eso nos va a permitir plantear tres ecuaciones con tres incógnitas:

Primero hallamos c:

Ahora, para hallar k y t:

Luego, como conocemos k, basta con sustituir arriba para hallar t:

O lo que es lo mismo, 2 horas 25 minutos y 6 segundos. Es decir, cuando llegó el forense hacía unas dos horas y media que había ocurrido la muerte, y por lo tanto, al llegar Grissom había pasado aproximadamente tres horas y media.

<Extraido de http://www.matematicasdigitales.com/matematicas-en-csi>

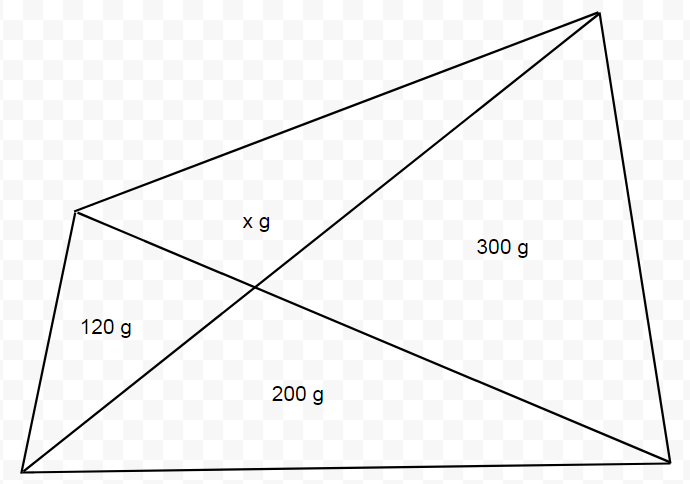
Tenemos una tarta con la forma del cuadrilátero ABCD y la dividimos en cuatro partes trazando las diagonales. Conocemos el peso de tres de los trozos y queremos averiguar el peso del cuarto trozo.

https://goo.gl/ohtngs