
Un problema de criptografía con matrices:
Emisor y receptor deciden utilizar la siguiente equivalencia para cifrar y descifrar un cierto mensaje confidencial:
a(1), b(2), c(3), d(4), e(5), f(6), g(7), h(8), i(9), j(10), k(11), l(12), m(13), n(14), o(15), p(16), q(17), r(18), s(19), t(20), u(21), v(22), w(23), x(24), y(25), z(26).
Dado que sería muy fácil, de este modo, descubrir el contenido del mensaje, acuerdan "desfigurarlo" multiplicando las sucesivas parejas de números asociados al texto por una matriz de orden dos; por ejemplo, por la matriz M de filas (2,1) y (1,1).
El receptor recibe el mensaje cifrado mkxs, y lo descifra. ¿Cuál es el mensaje original?
<Para profundizar en esta cuestión puedes visitar culturacientifica.com/2017/01/11/criptografia-matrices-cifrado-hill>
Publicado en El Mundo Today: "El valor de x se establece en 5 de una vez por todas. La medida permitirá ahorrar millones de cálculos al año".
Puesto que ya se ha despejado el valor de esta incógnita de forma definitiva, las horas lectivas de la asignatura de matemáticas en España, a partir de 1º de ESO, quedarán reducidas a una, pudiendo dedicar el resto de las horas a temas más relevantes. Los profesores de matemáticas temen ahora por sus trabajos.
"¿Y del valor de y se sabe algo?", preguntan los lectores.
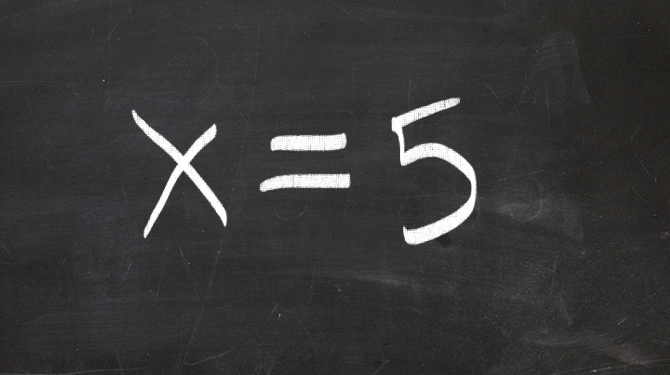
Una aplicación creada por Stephen Von Worley, científico y artista norteamericano, muestra gráficamente cada número como resultado de la multiplicación de números primos.
Como todos sabemos, los números de identificación que aparecen en los DNI, pasaportes, tarjetas de crédito, etc, llevan asociadas una cifra o letra, llamada dígito de control, que suele ir al final de la serie y que protege al número de cualquier tipo de error.
Los errores más frecuentes son de cuatro tipos:
-- Error simple: cambiar una cifra por otra.
-- Error de trasposición sin salto: alterar el orden de dos cifras consecutivas.
-- Error de trasposición con salto: alterar el orden de dos cifras no consecutivas.
-- Error doble: cambiar dos cifras por otras.
Dos herramientas matemáticas, el producto escalar y las clases residuales, son utilizadas en la "fabricación" de los dígitos de control. Veamos como ejemplo el caso de las tarjetas de crédito:
Página 85 de 93



