
Deprecated: Cannot use "parent" when current class scope has no parent in /home/u167666377/domains/sagradopontevedra.es/public_html/matematicas/administrator/components/com_fields/helpers/fields.php on line 608
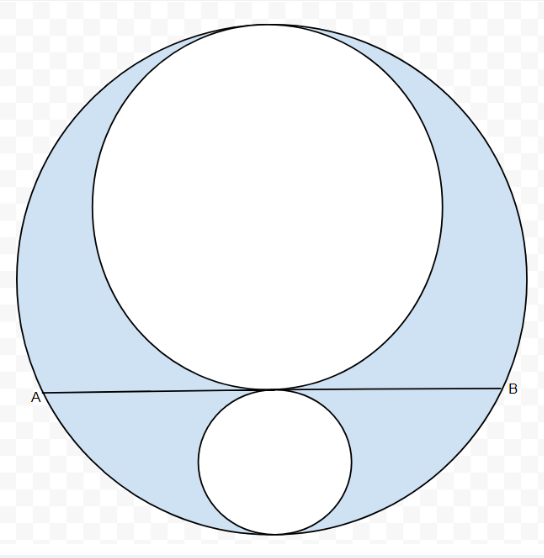
Tenemos dos circunferencias exteriores y tangentes entre si, interiores y tangentes a otra circunferencia de mayor tamaño. Calcula la cuerda de esta última circunferencia, AB, tangente simultáneamente a las dos primeras circunferencias, sabiendo que el área de la región comprendida entre las tres curvas es de 2.π cm2.
Uno de los desafíos matemáticos publicados por el periódico El País, en el año 2011, dice lo siguiente:
"Hace muchos siglos un pequeño grupo de antepasados nuestros buscaban un lugar adecuado donde establecerse y formar un poblado. Fue así como descubrieron un magnífico territorio llano en forma de triángulo equilátero de 10 km de lado. Era una tierra llena de posibilidades.
A lo largo de uno de los lados del triángulo, discurría un río tranquilo y cristalino de donde podían tomar el agua e incluso pescar. Otro de los lados se abría en toda su longitud a una sabana en donde podrían cazar buenas piezas. El tercer lado limitaba completamente con un terreno fértil que podían cultivar.
Felices con este descubrimiento se establecieron en un punto de esta vasta llanura triangular y construyeron tres caminos que unían el poblado con cada uno de los lados. Cada camino unía el poblado con uno de los lados en línea recta y de manera que el trayecto era el más corto posible. Y empezaron a vivir según sus ancestrales costumbres. Cada día, con el alba se dirigían al río a buscar agua e incluso algún pescado, si la suerte acompañaba. De regreso al poblado cambiaban los cántaros por los arcos y las flechas, y recorrían el camino hasta el límite de la sabana para cazar alguna presa que llevaban al poblado ante la alegría de todos. En la hoguera cocinaban sus manjares. Tras la comida y antes del trayecto vespertino, un poco de descanso. Por la tarde tomaban el camino hacia las zonas de cultivo para llevar a cabo rudimentarios trabajos agrícolas. Al atardecer volvían al poblado llevando, en ocasiones, el fruto de las sencillas cosechas.
Se trataba de una vida tranquila que sólo tenía el inconveniente de las largas caminatas de ida y vuelta en línea recta por los trillados caminos hacia el río, la sabana y los cultivos. Paso a paso, ni muy lentos ni muy rápidos, a una velocidad constante de 5 km/h, cada día recorrían los tres caminos que les aseguraban su sustento. Eran felices y vivían en paz... aunque a veces se sentían cansados de tanto caminar".
La pregunta es: ¿qué distancia recorre y cuántas horas emplea un individuo de esta tribu al hacer los tres recorridos de ida y vuelta? ¿Depende del punto en el que se encuentre el poblado?

https://es.wikipedia.org/wiki/Teorema_de_Viviani
En 1791, haciendo un alto en sus disputas políticas, la Asamblea Nacional Francesa define lo que con los años se convertirá en la medida de longitud universal: el metro. La diezmillonésima parte del cuadrante del meridiano terrestre.
Una pléyade de notables matemáticos como nunca antes habían convivido en Francia, va a vivir de forma intensa los acontecimientos de la Revolución Francesa: Joseph Louis Lagrange, Gaspard Monge, Peirre Simon de Laplace, Adrien Marie Legendre, y el marqués de Condorcet, van a llevar a la matemática francesa a su más alta cima.
Ellos van a poner los fundamentos científicos del Análisis, del cálculo de Probabilidades, de la Geometría descriptiva y de la Astronomía moderna. Pero van a hacer algo más: van a crear el modelo de la moderna enseñanza de las matemáticas superiores, un modelo que pervivirá más de dos siglos.
En 1858 el egiptólogo escocés A. Henry Rhind visitó Egipto por motivos de salud (padecía tuberculosis) y compró en Luxor el papiro que actualmente se conoce como papiro Rhind o de Ahmes, encontrado en las ruinas de un antiguo edificio de Tebas. Rhind murió 5 años después de la compra y el papiro fue a parar al Museo Británico. Desgraciadamente en esa época gran parte del papiro se había perdido, aunque 50 años después se encontraron muchos fragmentos en los almacenes de la Sociedad histórica de Nueva York. Actualmente se encuentra en el Museo Británico de Londres. Comienza con la frase "Cálculo exacto para entrar en conocimiento de todas las cosas existentes y de todos los oscuros secretos y misterios"
El papiro mide unos 6 metros de largo y 33 cm de ancho. Representa la mejor fuente de información sobre matemática egipcia que se conoce. Escrito en hierático, consta de 87 problemas y su resolución. Nos da información sobre cuestiones aritméticas básicas, fracciones, cálculo de áreas, volúmenes, progresiones, repartos proporcionales, reglas de tres, ecuaciones lineales y trigonometría básica. Fue escrito por el escriba Ahmes aproximadamente en el año 1650 a.C. a partir de escritos de 200 años de antigüedad, según reivindica el propio Ahmes al principio del texto.

<Artículo completo: http://www.egiptologia.org/ciencia/matematicas/papiro_rhind.htm>
Existen ciertos usos de la media aritmética que producen resultados totalmente erróneos. Lo aclaramos con un ejemplo muy simple sobre subida de precios: supongamos que en 3 años los precios de cierto producto han subido un 10%, un 20% y un 30% ¿Cuánto han subido en promedio? Obsérvese que para obtener el precio del primer año (tras una subida del 10%), tenemos que multiplicar por 1.1 el precio inicial. Al precio así obtenido tenemos que multiplicarlo por 1.2 (subida del 20%) para obtener el precio tras el segundo año. Y dicho precio hemos de multiplicarlo por 1.3 (subida del 30%) para obtener el precio final. Así, si el precio inicial es 100, el precio final será:
100 x (1.1) x (1.2) x (1.3) = 171.6
Sin embargo, si consideramos la media aritmética de 10%, 20% y 30% (o de 1.1, 1.2 y 1.3) obtenemos un porcentaje del 20% (o multiplicar por 1.2), pero si aplicamos esa subida del 20% cada año, el resultado que obtenemos será:
100 x (1.2) x (1.2) x (1.2) = 172.8
Así que no tiene sentido proporcionar la media aritmética para calcular la subida anual promediada de los precios de un artículo. En este caso tendríamos que haber calculado la media geométrica de los tres números: 1.1, 1.2 y 1.3.

Efectivamente si aplicamos cada año una subida del 19.721577 % obtenemos:
100 x (1.19721577) x (1.19721577) x (1.19721577) =171.6
que es el resultado correcto.

<Fuente: https://blogs.20minutos.es/mati-una-profesora-muy-particular/tag/media-geometrica>
Página 82 de 93
