En aguas de Florida, un capitán pirata saquea un galeón español y se adueña de un importante tesoro. Para esconderlo, elige una franja de la costa situada entre dos grandes rocas que le servirán de referencia. Una vez allí, ordena lo siguiente:
Dos hombres partirán del árbol solitario que se ve al fondo y caminarán hasta las rocas midiendo la distancia recorrida, en pasos. Al llegar, ambos girarán noventa grados tierra adentro y procederán a recorrer otro tanto. Entonces, se irán uno hacia el otro y a mitad del trayecto enterrarán el botín.
Años más tarde el capitán regresa a buscar su tesoro. Encuentra el lugar indicado por las rocas, pero se inquieta al ver que el árbol ha desaparecido. ¿Podrá encontrar el tesoro sin tener que cavar en toda la línea de la costa?
En la siguiente figura, A y B representan las rocas y C indica la posición del árbol:
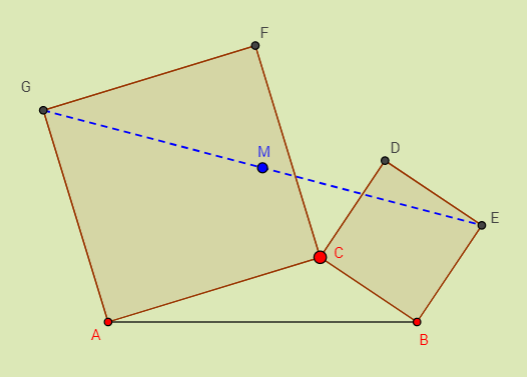
El problema propuesto está relacionado con el teorema de Bottema, que afirma lo siguiente:
"Si dibujamos dos cuadrados con un vértice común y trazamos el segmento que une los vértices más distantes, el punto medio de este segmento no depende de la posición del vértice que une dichos cuadrados". (¡Compruébalo!)


