Tres Patines, un genio de las matemáticas, te convencerá de que 28 entre 7 es 13:

Eva recibió una invitación para asistir a la fiesta que va a celebrar el Club de Pijos el último día de curso. No sabe si irá o no, pero haciendo indagaciones averiguó que, entre los pijos, la probabilidad de que uno de ellos sea divertido es mayor si tiene melena que si está pelado; es decir, P(divertido/melenudo) > P(divertido/pelado). Por tanto, si acudiera a la fiesta, ligaría con un melenudo.

Poco después la llamaron del Club de Macarras para invitarle a la fiesta que, por idéntico motivo, tiene pensado organizar dicho club ese mismo día, a la misma hora. Indagando sobre este grupo, llegó a conclusiones similares a las anteriores sobre la probabilidad de quien es más divertido: P(divertido/melenudo) > P(divertido/pelado). Así pues, si decidiera asistir, también ligaría con un melenudo.

Por ultimo, una nueva llamada le advierte de que pijos y macarras se habían puesto de acuerdo para hacer una única fiesta ese día. Revisando sus notas, Eva descubre con asombro que en el conjunto de todos ellos las cosas cambian radicalmente; es decir, P(divertido/melenudo) < P(divertido/pelado). Por tanto, ¡tendrá que cambiar su estrategia y ligar con un pelado!

¿Cómo es posible que sea así? Observa el siguiente ejemplo y te convencerás: https://goo.gl/Rcc3ie

La barra roja genera, al girar, un hiperboloide de una sola hoja. Si hacemos pasar un plano por el eje del hiperboloide, observaremos que dicha barra atraviesa "limpiamente" la hipérbola generatriz.

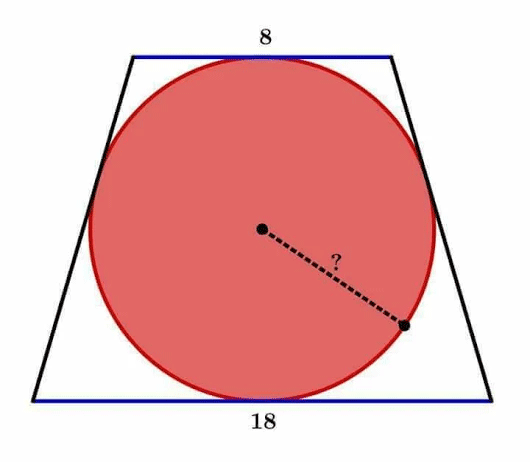
En un trapecio isósceles, de bases 8 y 18 unidades, se inscribe una circunferencia. Halla el radio de dicha circunferencia.