Los lados de un triángulo están en progresión geométrica de razón r . ¿Qué valores puede tomar dicha razón?
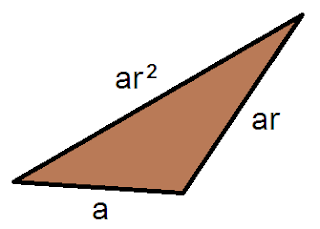
El lado mayor de un triángulo es menor que la suma de los otros dos. Entonces:
--- Si r > 1 , a < ar < ar2 . Y por lo tanto
a + ar > ar2
1 + r > r2
r2 – r – 1 < 0
1 < r < (1+√5)/2 = φ
La razón de la progresión tiene que ser menor que la razón áurea φ = 1,618...
--- Si r < 1 , a > ar > ar2 . Y por lo tanto
a < ar + ar2
1 < r + r2
r2 + r – 1 > 0
1 > r > (–1+√5)/2 = 1/φ
La razón de la progresión tiene que ser mayor que 1/φ = 0,618...
Concluyendo:
1/φ < r < φ


