El teorema de Pick relaciona el área de un polígono simple cuyos vértices tienen coordenadas enteras con el número de puntos en su interior y en su borde que tengan también coordenadas enteras.  

Consideremos entonces un polígono simple cuyos vértices tengan coordenadas enteras. El teorema establece lo siguiente: 

Si B es el número de puntos de coordenadas enteras en el borde del polígono e I el número de puntos de coordenadas enteras en su interior, entonces el área (A) de dicho polígono viene dada por la fórmula: 

Veamos un ejemplo: 

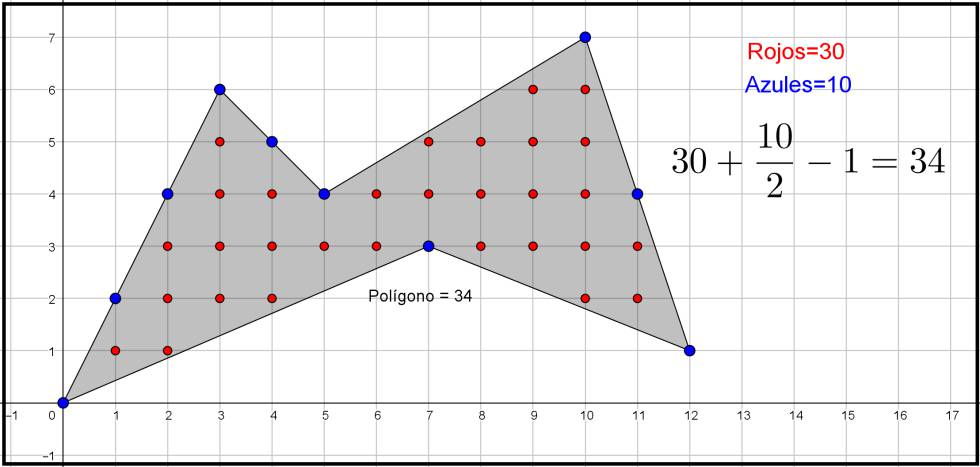
 <https://elpais.com/elpais/2017/11/08/el_aleph/1510158827_253966.html>