El principio del palomar, también llamado principio de Dirichlet, establece que si n palomas se distribuyen en m palomares y n > m, entonces habrá al menos un palomar con más de una paloma.  Resulta evidente que si tenemos que colocar unas cuantas palomas en palomares y tenemos más palomas que palomares, entonces en (al menos) un palomar habrá más de una paloma.

Un ejemplo sencillo de aplicación de este principio: 

Si consideremos un triángulo equilátero de 2 m de lado y dibujamos 5 puntos dentro de él, siempre ocurrirá que al menos dos de esos puntos distarán entre sí menos de 1 m.

Es evidente que los cinco puntos dibujados son las palomas. Por otro lado, si unimos los puntos medios de los lados del triángulo equilátero considerado, se obtienen otros cuatro triángulos equiláteros, de 1 m de lado, que serían los palomares. Como hay más palomas que palomares, al menos dos de los cinco puntos estarán dentro de uno de los triángulos pequeños, es decir, a menos de 1 metro de distancia, uno del otro.

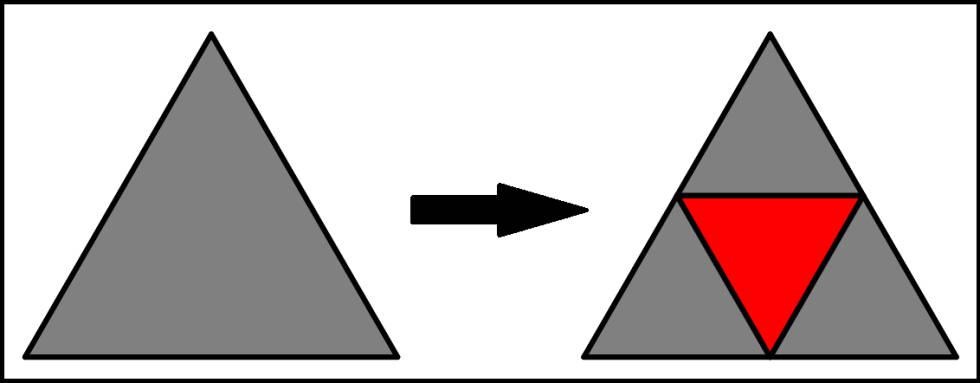
<Fuente: https://elpais.com/elpais/2017/01/10/el_aleph/1484088947_059937.html>