Imaginemos que dos personas han pedido una pizza, por ejemplo, mediana. Cuando les entreguen la pizza, esta estará cortada en ocho trozos y en condiciones ideales, es decir, que los cuatro cortes pasen por el centro y estén igualmente espaciados, lo que significa que están formando un ángulo de 45º entre cada dos de ellos, estos serán completamente iguales (como en la imagen). En tal caso, será fácil repartir la pizza, cada comensal simplemente tendrá que coger cuatro trozos cualesquiera.

Pero lo normal es que esos cortes realizados en la pizzería no sean tan perfectos. Supongamos que aún así los cuatro cortes pasan por un punto común, aunque no sea el centro del círculo que forma la pizza, y que estén igualmente espaciados, es decir, formando un ángulo de 45º entre cada dos de los cortes consecutivos. Un ejemplo de esta situación se muestra en la siguiente imagen:

La cuestión ahora es si es posible repartir la pizza, sin realizar más cortes, de forma que cada una de las dos personas reciba la misma cantidad de la misma. Mirando la imagen de la pizza cortada de esta forma no da la impresión de que sea posible repartir los trozos de manera equitativa; sin embargo, el conocido como Teorema de la pizza nos dice que sí es posible.

Teorema de la pizza: Si una pizza es dividida en ocho trozos, obtenidos mediante cuatro cortes que pasan por un punto común y forman un ángulo de 45º entres ellos, entonces la suma de las áreas de los trozos alternos son iguales. (Es decir, son iguales las áreas de los trozos grises y blancos, en la imagen anterior).

Esta cuestión fue originalmente propuesta por el matemático L. J. Upton en Mathematics Magazine, problema 660, en 1967, y resuelta por Michael Goldberg también en Mathematics Magazine.

Larry Carter y Stan Wagon realizaron una demostración visual por medio de disecciones que fue recogida en el libro Proofs without Words II, de Roger B. Nelsen  y que reproducimos aquí. Os dejamos que observéis el diagrama y comprobéis por vosotros mismos que efectivamente los trozos grises y blancos tienen la misma superficie total, viendo que los nuevos trozos más pequeños generados por Carter y Wagon mediante cortes de los anteriores se corresponden dos a dos en superficie.

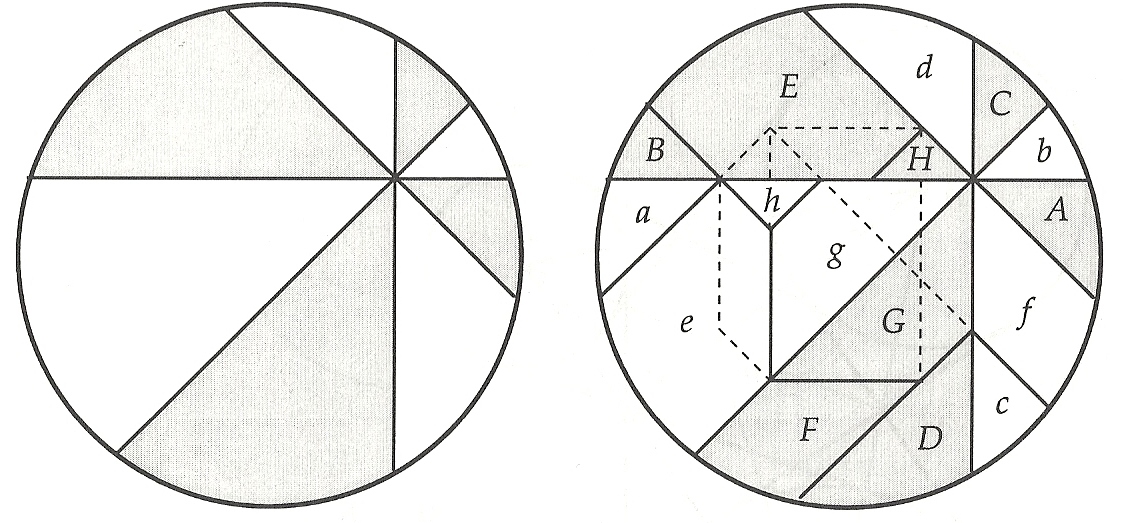
El resultado del teorema de la pizza es cierto para un número de cortes par mayor que 2, es decir, 4, 6, 8, etc., y por lo tanto, con un número de trozos de pizza mayor que 4 y múltiplo de 4, es decir, 8, 12, 16, etc. 

<Artículo completo: https://culturacientifica.com/2013/09/11/el-teorema-de-la-pizza>

La cosa va de cuadrados mágicos vistos como matrices. Vamos a tomar el  cuadrado mágico 3×3 que forman los números naturales 1, 2, 3,..., 9 y veámoslo como una matriz 3×3:

¿Qué pasa si lo multiplicamos por sí mismo como se multiplican habitualmente las matrices?:

Pasa que si sumamos las filas y las columnas, obtenemos el mismo resultado, 225, pero al sumar los elementos de las diagonales eso no ocurre. Lástima, no nos ha quedado un cuadrado mágico…pero no desistamos. Multipliquemos ahora el resultado de nuevo por A:

Sumad ahora filas, columnas y diagonales…Éste sí es un cuadrado mágico. Todas las filas, todas las columnas y las dos diagonales suman 3375. Es decir, para esta matriz mágica A tenemos que  también es una matriz mágica.

Si calculamos  no obtenemos una matriz mágica, pero podéis comprobar que  sí lo es. En general, toda potencia impar de la matriz mágica A vuelve a ser una matriz mágica.

En general, toda matriz mágica 3×3 cumple que sus potencias impares son también matrices mágicas.

Esta propiedad no sólo se cumple con potencias impares de la misma matriz mágica, sino que se cumple con cualquier producto de un número impar de matrices mágicas 3×3. Además, no importa el orden en el que hagamos esos productos, (recordad que el producto de matrices no es conmutativo, por lo que el orden al multiplicar podría influir). Os dejo un ejemplo:

<Artículo completo: https://www.gaussianos.com/maravillas-que-te-encuentras-cuando-juegas-con-cuadrados-magicos>

Dado un rectángulo ABCD, con el lado AB menor que AD, halla un punto E sobre el lado AD desde el cual se vean los lados AB y BC bajo el mismo ángulo.

<Visto en https://goo.gl/M21v3g>

Precursor de la fotografía callejera, René Maltête fue un fotógrafo francés y poeta, nacido en 1930 y fallecido en el año 2000. Con la ilusión de convertirse en un director de cine, René capturó con su cámara fotográfica las escenas inusuales de la vida cotidiana de una forma inteligente y divertida. Supo plasmar la ciudad y los transeúntes imaginando las interacciones entre las cosas y personas.